题目内容
已知B为线段MN上一点,|MN|=6,|BN|=2,过B作⊙C与MN相切,分别过M,N作⊙C的切线交于P点,则P的轨迹是 .
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:如图所示,以MN所在直线为x轴,MN的垂直平分线为y轴,O为坐标原点,建立坐标系.设MP,NP分别与⊙C相切于D,E两点,利用圆的切线的性质可得:|PM|-|PN|=|DM|-|EN|=|MB|-|BN|=6-2-2=2<|MN|.利用双曲线的定义即可判断出.
解答:
解:如图所示,
以MN所在直线为x轴,MN的垂直平分线为y轴,O为坐标原点,建立坐标系.
设MP,NP分别与⊙C相切于D,E两点,
则|PM|-|PN|=|DM|-|EN|=|MB|-|BN|=6-2-2=2<|MN|.
∴点P的轨迹是以M,N为焦点,2a=2,2c=6的双曲线的右支(顶点除外).
∴点P的轨迹方程为:x2-
=1(x>1).
故答案为:x2-
=1(x>1).

以MN所在直线为x轴,MN的垂直平分线为y轴,O为坐标原点,建立坐标系.
设MP,NP分别与⊙C相切于D,E两点,
则|PM|-|PN|=|DM|-|EN|=|MB|-|BN|=6-2-2=2<|MN|.
∴点P的轨迹是以M,N为焦点,2a=2,2c=6的双曲线的右支(顶点除外).
∴点P的轨迹方程为:x2-
| y2 |
| 8 |
故答案为:x2-
| y2 |
| 8 |
点评:本题考查了圆的切线的性质、双曲线的定义及其标准方程,考查了推理能力,属于中档题.

练习册系列答案
相关题目
若正数a,b,c成公差不为零的等差数列,则( )
| A、lga,lgb,lgc成等差数列 |
| B、lga,lgb,lgc成等比数列 |
| C、2a,2b,2c成等差数列 |
| D、2a,2b,2c成等比数列 |
若某多面体的三视图如图所示,则此多面体外接球的表面积是( )


| A、6 | ||||
B、
| ||||
| C、12π | ||||
| D、3π |
某几何体的三视图如图所示,则该几何体的表面积为( )


A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
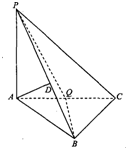 在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上,
在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上,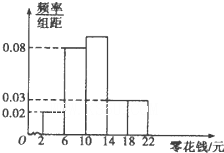 一所中学共有4000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有
一所中学共有4000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有