题目内容
已知抛物线x2=8y的准线经过双曲线
-x2=1的一个焦点,则该双曲线的离心率为 .
| y2 |
| m2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出排趋性的准线方程,得到双曲线的焦点坐标,然后求解双曲线的离心率即可.
解答:
解:抛物线x2=8y的准线方程为:y=-2,所以双曲线中c=2,由双曲线
-x2=1方程可得:m2+1=4,解得:m=
,
∴双曲线的离心率为:e=
=
.
故答案为:
.
| y2 |
| m2 |
| 3 |
∴双曲线的离心率为:e=
| c |
| a |
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查双曲线的简单性质的以及抛物线的简单性质的应用,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
| A、“f(O)=O”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、“向量a,b,c,若a•b=a•c,则b=c”是真命题 | ||||||||
C、函数f(x)=
| ||||||||
D、“若α=
|
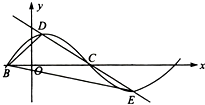 已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(
已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(| BD |
| BE |
| BE |
| CE |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、2 |
下列命题中的真命题是( )
A、?x∈R,sinx+
| ||
B、?x∈R,
| ||
| C、命题p:“?x∈R,x2-x-1>0”的否定¬p:“?x∈R,x2-x-1≤0” | ||
| D、“ea>eb”是“log2a>log2b”的充要条件 |
阅读下面程序框图,则输出结果s的值为( )


A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
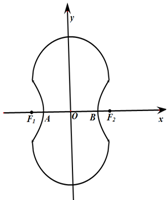 如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶
如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶