题目内容
某几何体的三视图如图所示,则该几何体的表面积为( )


A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:上面是一个圆锥的一半,下面是一个半球.即可得出.
解答:
解:由三视图可知:上面是一个圆锥的一半,下面是一个半球.
∴该几何体的表面积S=
×4π×12+
×π×12+
×π×1×
+
×2×1
=
π+1.
故选:D.
∴该几何体的表面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
=
5+
| ||
| 2 |
故选:D.
点评:本题考查了圆锥与球的表面积计算公式,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
阅读下面程序框图,则输出结果s的值为( )


A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
若复数z满足zi=1-i(i为虚数单位),则复数z等于( )
| A、1+i | B、-1-i |
| C、1-i | D、-1+i |
如图所示的程序框图中输出的结果为( )


| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a,b是方程x2+x+c=0的两个实根,且0≤c≤
,则这两条直线之间的距离的最大值和最小值分别是( )
| 1 |
| 8 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
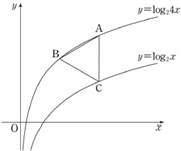 如图所示,已知函数 y=log24x图象上的两点 A、B 和函数 y=log2x上的点 C,线段 AC平行于 y 轴,三角形 ABC 为正三角形时,点B的坐标为 (p,q),则 p2×2q的值为
如图所示,已知函数 y=log24x图象上的两点 A、B 和函数 y=log2x上的点 C,线段 AC平行于 y 轴,三角形 ABC 为正三角形时,点B的坐标为 (p,q),则 p2×2q的值为