题目内容
已知函数f(x)=
,数列{an}是首项等于1且公比等于f(1)的等比数列;数列{bn}首项b1=
,满足递推关系bn+1=f(bn).
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=
,求数列{cn}的前n项和Tn.
| x |
| 3x+1 |
| 1 |
| 3 |
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=
| an |
| bn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)直接根据已知条件求出数列的通项公式.
(Ⅱ)利用上步的结论,使用乘公比错位相减法求出结果.
(Ⅱ)利用上步的结论,使用乘公比错位相减法求出结果.
解答:
解:(Ⅰ)函数f(x)=
,
则:f(1)=
由于:数列{an}是首项等于1且公比等于f(1)的等比数列,
所以:an=(
)n-1
数列{bn}首项b1=
,满足递推关系bn+1=f(bn).
则:bn+1=
整理得:
-
=3
所以:{
}是以
=
为首项,3为公差的等差数列.
解得:bn=
(Ⅱ)cn=
=3n•(
)n-1
则:Tn=c1+c2+…+cn=3•(
)0+6•(
)1+…+3n•(
)n-1n-1①
Tn=3•(
)1+6•(
)2+…+3n•(
)nn②
则:①-②得:
Tn=3•
-
=4-
所以:Tn=
-
| x |
| 3x+1 |
则:f(1)=
| 1 |
| 4 |
由于:数列{an}是首项等于1且公比等于f(1)的等比数列,
所以:an=(
| 1 |
| 4 |
数列{bn}首项b1=
| 1 |
| 3 |
则:bn+1=
| bn |
| 3bn+1 |
整理得:
| 1 |
| bn+1 |
| 1 |
| bn |
所以:{
| 1 |
| bn |
| 1 |
| b1 |
| 1 |
| 3 |
解得:bn=
| 1 |
| 3n |
(Ⅱ)cn=
| an |
| bn |
| 1 |
| 4 |
则:Tn=c1+c2+…+cn=3•(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
则:①-②得:
| 3 |
| 4 |
1-(
| ||
1-
|
| 3n |
| 4n |
| 4+3n |
| 4n |
所以:Tn=
| 16 |
| 3 |
| 3n+4 |
| 3•4n-1 |
点评:本题考查的知识要点:数列通项公式的求法,乘公比错位相减法的应用,属于基础题型.

练习册系列答案
相关题目
已知函数f(x)=x2+mx-2n,m,n∈[0,2],则使f(1)≤0成立的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
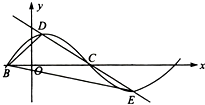 已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则
已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则