题目内容
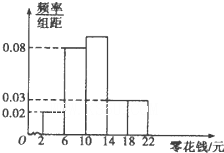一所中学共有4000名学生，为了引导学生树立正确的消费观，需抽样调查学生每天使用零花钱的数量（取整数元）情况，分层抽取容量为300的样本，作出频率分布直方图如图所示，请估计在全校所有学生中，一天使用零花钱在6元～14元的学生大约有考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图求出对应的频率与频数，即可估计出结果．
解答：
解：根据频率分布直方图得；
一天使用零花钱在6元～14元的学生频率是
1-（0.02+0.03+0.03）×4=1-0.32=0.68，
∴对应的频数是4000×0.68=2720；
∴估计全校学生中，一天使用零花钱在6元～14元的大约有2720人．
一天使用零花钱在6元～14元的学生频率是
1-（0.02+0.03+0.03）×4=1-0.32=0.68，
∴对应的频数是4000×0.68=2720；
∴估计全校学生中，一天使用零花钱在6元～14元的大约有2720人．
点评：不同考查了频率分布直方图的应用问题，也考查了频率、频数与样本容量的关系，是基础题．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
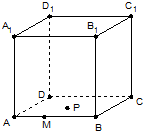如图，正方体ABCD-A1B1C1D1的棱长为1，点M在棱AB上，且PB，点AM=| 1 |
| 3 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
已知平面α∥平面β，直线m?平面α，那么直线m与平面β 的关系是（ ）
| A、直线m在平面β内 |
| B、直线m与平面β相交但不垂直 |
| C、直线m与平面β垂直 |
| D、直线m与平面β平行 |
下列说法正确的是（ ）
| A、“f（O）=O”是“函数f（x）是奇函数”的充要条件 | ||||||||
| B、“向量a，b，c，若a•b=a•c，则b=c”是真命题 | ||||||||
C、函数f（x）=
| ||||||||
D、“若α=
|
下列命题中的真命题是（ ）
A、?x∈R，sinx+
| ||
B、?x∈R，
| ||
| C、命题p：“?x∈R，x2-x-1＞0”的否定￢p：“?x∈R，x2-x-1≤0” | ||
| D、“ea＞eb”是“log2a＞log2b”的充要条件 |
如图所示的程序框图中输出的结果为（ ）
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|