Question

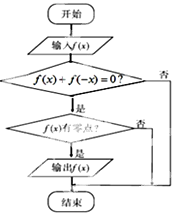
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（　　）

• A、f（x）=cos2x
• B、f（x）=

  4x+1

  2x

• C、f（x）=ln（

  x2+1

  -x）
• D、f（x）=

  1-x2

Answer 1

考点：程序框图

专题：图表型

分析：根据流程图，依次判断4个选择项是否满足输出函数的条件即可得到答案．

解答： 解：由框图可判断出框图的功能是输出的函数f（x）既是奇函数又存在零点
A，f（x）=cos2x为偶函数，f（x）+f（-x）=0不成立，由流程图可知，不能输出函数．
B，显然f（-x）=-f（x）不成立，故由流程图可知，不能输出函数．
C，函数f（x）=ln（

x2+1

-x）可以输出，验证f（-x）=ln

(-x)2+1

-(-x)=-f（x）发现，函数是奇函数且当x=0时函数值为0，故正确；
D，函数不能输出，因为它是偶函数，不是奇函数．
故选：C．

点评：本题考查选择结构，解答本题的关键是根据框图得出函数所满足的性质，然后比对四个选项中的函数，对四个函数的性质比较了解也是判断出正确答案的关键，属于基本知识的考查．