题目内容
若函数f（x）=x•（x-c）2在x=2处有极大值，则常数c的值为（ ）
| A、6 | ||
| B、2 | ||
| C、2或6 | ||
D、
|
考点：利用导数研究函数的极值
专题：计算题,导数的综合应用
分析：由题意求导并令导数为0，即（2-c）2+4（2-c）=0，从而解出c，再检验即可．
解答：
解：∵f′（x）=（x-c）2+2x（x-c），
∵函数f（x）=x•（x-c）2在x=2处有极大值，
∴（2-c）2+4（2-c）=0，
解得c=2或c=6；
经检验，c=6，
故选A．
∵函数f（x）=x•（x-c）2在x=2处有极大值，
∴（2-c）2+4（2-c）=0，
解得c=2或c=6；
经检验，c=6，
故选A．
点评：本题考查了导数的应用，属于中档题．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
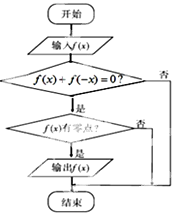
| A、f（x）=cos2x | ||
B、f（x）=
| ||
C、f（x）=ln（
| ||
D、f（x）=
|
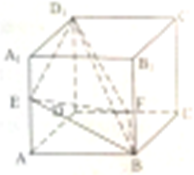如图，已知正方体ABCD-A1B1C1D1棱长为1，E，F分别为AA1，CD的中点，则四面体D1EBF的体积为已知数列{an}的前n项和Sn=n2+n+1，则a1+a9等于（ ）
| A、19 | B、20 | C、21 | D、22 |
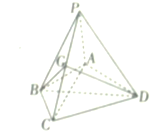如图，在四棱锥P-ABCD中，BD⊥PC，AB=BC=2，AD=CD=