题目内容
已知m,k∈Z,且方程mx2-kx+2=0在(0,1)上有两个不同的实数根,则m+k的最小值为 .
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:设出f(x)=mx2-kx+2,由f(0)=2,易知f(x)的图象恒过定点(0,2),将一元二次方程的根的分布转化为确定相应的二次函数的图象处理,根据图象可得到关于m和k的不等式组,此时不妨考虑利用不等式所表示的平面区域解决,但须注意这不是线性规划问题,同时注意取整点.
解答:
 解:设f(x)=mx2-kx+2,由f(0)=2,易知f(x)的图象恒过定点(0,2),
解:设f(x)=mx2-kx+2,由f(0)=2,易知f(x)的图象恒过定点(0,2),
因此要使已知方程在区间(0,1)内两个不同的根,即f(x)的图象在区间(0,1)内与x轴有两个不同的交点即由题意可以得到:必有
,即
,
在直角坐标系中作出满足不等式平面区域,
如图所示,设z=m+k,则直线m+k-z=0经过图中的阴影中的整点(6,7)时,
z=m+k取得最小值,即zmin=13.
故答案为13.
 解:设f(x)=mx2-kx+2,由f(0)=2,易知f(x)的图象恒过定点(0,2),
解:设f(x)=mx2-kx+2,由f(0)=2,易知f(x)的图象恒过定点(0,2),因此要使已知方程在区间(0,1)内两个不同的根,即f(x)的图象在区间(0,1)内与x轴有两个不同的交点即由题意可以得到:必有
|
|
在直角坐标系中作出满足不等式平面区域,
如图所示,设z=m+k,则直线m+k-z=0经过图中的阴影中的整点(6,7)时,
z=m+k取得最小值,即zmin=13.
故答案为13.
点评:本题考查了一元二次方程根的分布,结合函数图象以及平面区域解答.

练习册系列答案
相关题目
设a,b∈R,则“a≥1且“b≥1”是“a+b≥2”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
若直线y=x+b与曲线x=
恰有一个公共点,则b的取值范围是( )
| 1-y2 |
| A、-1<b≤1 | ||
| B、-1≤b≤1 | ||
C、-
| ||
D、-1<b≤1或b=-
|
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
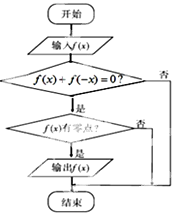

| A、f(x)=cos2x | ||
B、f(x)=
| ||
C、f(x)=ln(
| ||
D、f(x)=
|
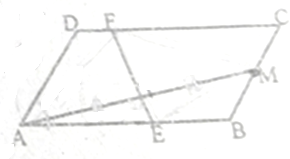 已知,平行四边形ABCD中,AB=4,AD=2
已知,平行四边形ABCD中,AB=4,AD=2