题目内容
已知动点P到点F(2,0)的距离与到直线l:x=
的距离之比为2.
(1)求点P的轨迹C的方程;
(2)直线l的方程为x+y-2=0,l与曲线C交于A,B两点,求线段AB的长.
| 1 |
| 2 |
(1)求点P的轨迹C的方程;
(2)直线l的方程为x+y-2=0,l与曲线C交于A,B两点,求线段AB的长.
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设出P的坐标,利用已知条件得到方程化简求解即可求点P的轨迹C的方程;
(2)直线l的方程为x+y-2=0,l与曲线C联立方程组,利用韦达定理以及弦长公式,即可求线段AB的长.
(2)直线l的方程为x+y-2=0,l与曲线C联立方程组,利用韦达定理以及弦长公式,即可求线段AB的长.
解答:
解:(1)设点P的坐标为(x,y),则由题意得
=2,…(2分)
化简得x2-
=1,即为点P的轨迹C的方程.…(6分)
(2)将y=-x+2代入x2-
=1中,并化简得:2x2+4x-7=0,…(8分)
A,B两点的坐标分别为:(x1,y1),(x2,y2),
由韦达定理可得x1+x2=-2,x1x2=-
,
所以|AB|=
=6.…(12分)
| ||
| x-
|
化简得x2-
| y2 |
| 3 |
(2)将y=-x+2代入x2-
| y2 |
| 3 |
A,B两点的坐标分别为:(x1,y1),(x2,y2),
由韦达定理可得x1+x2=-2,x1x2=-
| 7 |
| 2 |
所以|AB|=
| 2 |
| (x1+x2)2-4x1x2 |
点评:本题考查轨迹方程的求法,直线与圆锥曲线的位置关系的应用,考查计算能力以及转化思想的应用.

练习册系列答案
相关题目
若直线y=x+b与曲线x=
恰有一个公共点,则b的取值范围是( )
| 1-y2 |
| A、-1<b≤1 | ||
| B、-1≤b≤1 | ||
C、-
| ||
D、-1<b≤1或b=-
|
设等差数列{an}满足:
=1,公差d∈(-1,0).若当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| sin2a3-cos2a3+cos2a3cos2a6-sin2a3sin2a6 |
| sin(a4+a5) |
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
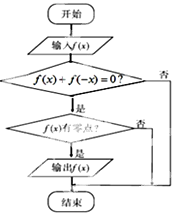

| A、f(x)=cos2x | ||
B、f(x)=
| ||
C、f(x)=ln(
| ||
D、f(x)=
|
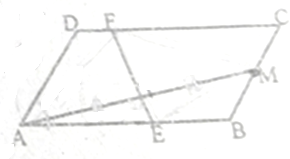 已知,平行四边形ABCD中,AB=4,AD=2
已知,平行四边形ABCD中,AB=4,AD=2