题目内容
等比数列{an}中,前n项和满足S5=10,S10=50,则S15=( )
| A、210 | B、250 |
| C、310 | D、350 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:先根据{an}为等比数列判断出S5,S10-S5,S15-S10,进而求得10,40,S15-50也为等比数列,利用等比中项的性质求得S15.
解答:
解:∵数列{an}为等比数列,
∴S5,S10-S5,S15-S10,也为等比数列,
∵S5=10,S10=50,
∴10,40,S15-50也为等比数列,
∴S15=210,
故选:A
∴S5,S10-S5,S15-S10,也为等比数列,
∵S5=10,S10=50,
∴10,40,S15-50也为等比数列,
∴S15=210,
故选:A
点评:本题考查等比数列的通项公式和前n项和公式的应用,解题时要认真审题,仔细解答,注意等比中项公式的应用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
设等差数列{an}满足:
=1,公差d∈(-1,0).若当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| sin2a3-cos2a3+cos2a3cos2a6-sin2a3sin2a6 |
| sin(a4+a5) |
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
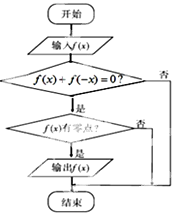

| A、f(x)=cos2x | ||
B、f(x)=
| ||
C、f(x)=ln(
| ||
D、f(x)=
|
设函数f(x)在(0,+∞)上是增函数,a=f(2
),b=f(log2
)的大小( )
| 3 |
| 2 |
| 3 |
| 2 |
| A、a>b | B、a<b |
| C、a≥b | D、a≤b |
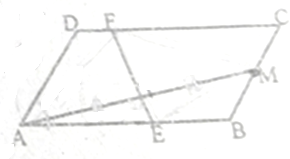 已知,平行四边形ABCD中,AB=4,AD=2
已知,平行四边形ABCD中,AB=4,AD=2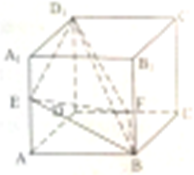 如图,已知正方体ABCD-A1B1C1D1棱长为1,E,F分别为AA1,CD的中点,则四面体D1EBF的体积为
如图,已知正方体ABCD-A1B1C1D1棱长为1,E,F分别为AA1,CD的中点,则四面体D1EBF的体积为