题目内容
设公差不为0的等差数列{an}的首项为1,且a2,a5,a14构成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=
,求数列{bn}的前2n项和T2n.
(1)求数列{an}的通项公式;
(2)设bn=
|
考点:数列的求和
专题:等差数列与等比数列
分析:(1)直接根据已知条件,建立等量关系求出数列的通项公式.
(2)利用分类的方法和裂项相消的方法求数列的和.
(2)利用分类的方法和裂项相消的方法求数列的和.
解答:
解:(1)设等差数列{an}的公差为d(d≠0),
∵a2,a5,a14构成等比数列,
∴a22=a2a14,
即(1+4d)2=(1+d)(1+13d),
解得d=0(舍去),或d=2.
∴an=1+(n-1)×2=2n-1.
(2)由(Ⅰ)得bn=
①当n为奇数时,bn=
=2(
-
),
②当n为偶数时,bn是等比数列,直接利用求和公式求解.
所以T2n=2(1-
+
-
+…+
-
)+15(21+25+…+24n-3)
=2-
+15×
=24n+1-
.
∵a2,a5,a14构成等比数列,
∴a22=a2a14,
即(1+4d)2=(1+d)(1+13d),
解得d=0(舍去),或d=2.
∴an=1+(n-1)×2=2n-1.
(2)由(Ⅰ)得bn=
|
①当n为奇数时,bn=
| 4 |
| n(n+2) |
| 1 |
| n |
| 1 |
| n+2 |
②当n为偶数时,bn是等比数列,直接利用求和公式求解.
所以T2n=2(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=2-
| 2 |
| 2n+1 |
| 2(1-16n) |
| 1-16 |
| 2 |
| 2n+1 |
点评:本题考查的知识要点:数列通项公式的求法,利用分类法求数列的和,裂项相消法求数列的和.属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
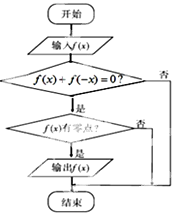

| A、f(x)=cos2x | ||
B、f(x)=
| ||
C、f(x)=ln(
| ||
D、f(x)=
|
设函数f(x)在(0,+∞)上是增函数,a=f(2
),b=f(log2
)的大小( )
| 3 |
| 2 |
| 3 |
| 2 |
| A、a>b | B、a<b |
| C、a≥b | D、a≤b |
已知整数x,y满足
,设z=x-3y,则( )
|
| A、z的最大值为1 |
| B、z的最小值为1 |
| C、z的最大值为2 |
| D、z的最小值为2 |
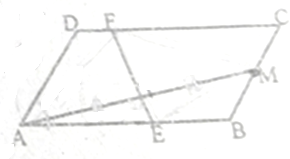 已知,平行四边形ABCD中,AB=4,AD=2
已知,平行四边形ABCD中,AB=4,AD=2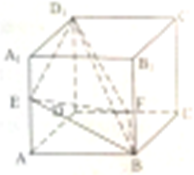 如图,已知正方体ABCD-A1B1C1D1棱长为1,E,F分别为AA1,CD的中点,则四面体D1EBF的体积为
如图,已知正方体ABCD-A1B1C1D1棱长为1,E,F分别为AA1,CD的中点,则四面体D1EBF的体积为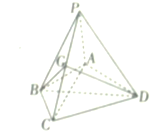 如图,在四棱锥P-ABCD中,BD⊥PC,AB=BC=2,AD=CD=
如图,在四棱锥P-ABCD中,BD⊥PC,AB=BC=2,AD=CD=