题目内容
已知函数f（x）=log2（2-ax）在（-∞，1]上单调递减，则a的取值范围是（ ）
| A、1＜a＜2 |
| B、0＜a＜1 |
| C、0＜a＜1或1＜a＜2 |
| D、0＜a＜1或a＞2 |
考点：对数函数的图像与性质
专题：函数的性质及应用
分析：题目给出的函数是复合函数，外层函数对数函数是增函数，要使复合函数在（-∞，1]调递减，需要内层函数在（-∞，1]上单调递减，可知a＞1，同时保证在x=1时，2-ax大于等于0，由此列不等式组求解a的取值范围．
解答：
解：令t=2-ax，则原函数化为g（t）=log2t，
外层函数g（t）=log2t为增函数，
要使复合函数f（x）=log2（2-ax）（-∞，1]上单调递减，
则内层函数t=2-ax在（-∞，1）上单调递减，且
t=2-ax在（-∞，1）上大于0恒成立．
∴
，
解得：1＜a＜2．
∴a的取值范围是（1，2）
故选：A
外层函数g（t）=log2t为增函数，
要使复合函数f（x）=log2（2-ax）（-∞，1]上单调递减，
则内层函数t=2-ax在（-∞，1）上单调递减，且
t=2-ax在（-∞，1）上大于0恒成立．
∴
|
解得：1＜a＜2．
∴a的取值范围是（1，2）
故选：A
点评：本题考查了复合函数的单调性，考查了数学转化思想方法，因内层函数为减函数，此题是中档题．
练习册系列答案
相关题目
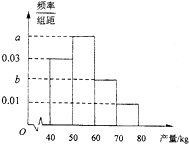果农随机选取某类果树50株作为样本测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，50]，（50，60]，（60，70]，（70，80]进行分组，得到频率分布直方图如图，已知样本中产量在区间（50，60]上的果树株数是产量在区间（60，80]上的果树株数的已知x，y满足
，则x2+y2的最大值为（ ）
|
| A、5 | B、9 | C、16 | D、25 |
已知集合M={y|y=-x2+1，x∈R}，N={y|y=x2，x∈R}，全集I=R，则M∪N等于（ ）
A、{（x，y）|x=±
| ||||||
B、{（x，y）|x≠±
| ||||||
| C、{y|y≤0，或y≥1} | ||||||
| D、R |
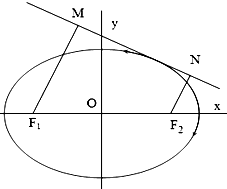设点F1（-c，0），F2（c，0）分别是椭圆C：