题目内容
已知
,求z=2y-2x+4的最大值及最小值.
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出题中不等式组表示的平面区域,根据平面区域将目标函数对应的直线进行平移并观察z的变化,即可得目标函数的最小值与最大值.
解答:
解:作出约束条件
表示的平面区域,
如图所示;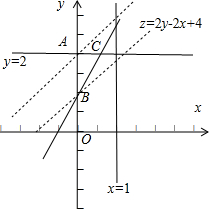
平面区域是△ABC及其内部,其中A(0,2),B(0,1),C(
,2);
将直线l:z=2y-2x+4进行平移,
当l经过点A时,目标函数z达到最大值,
l经过点B时,目标函数z达到最小值;
∴z最大值=2×2-2×0+4=8,
z最小值=2×1-2×0+4=6;
∴z=2y-2x+4的最大值是8,最小值是6.
|
如图所示;

平面区域是△ABC及其内部,其中A(0,2),B(0,1),C(
| 1 |
| 2 |
将直线l:z=2y-2x+4进行平移,
当l经过点A时,目标函数z达到最大值,
l经过点B时,目标函数z达到最小值;
∴z最大值=2×2-2×0+4=8,
z最小值=2×1-2×0+4=6;
∴z=2y-2x+4的最大值是8,最小值是6.
点评:本题考查了给出二元一次不等式组,求目标函数最值的问题,解题时应画出二元一次不等式组表示的平面区域,再求最优解与目标函数的最值,是基础题.

练习册系列答案
相关题目
已知集合M={y|y=-x2+1,x∈R},N={y|y=x2,x∈R},全集I=R,则M∪N等于( )
A、{(x,y)|x=±
| ||||||
B、{(x,y)|x≠±
| ||||||
| C、{y|y≤0,或y≥1} | ||||||
| D、R |
在△ABC中,若AB=2,AC2+BC2=8,则△ABC面积的最大值为( )
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
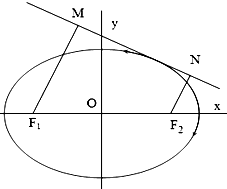 设点F1(-c,0),F2(c,0)分别是椭圆C:
设点F1(-c,0),F2(c,0)分别是椭圆C: