题目内容
已知直线L:(a2+1)x+2ay+1=0(a>0),求直线斜率和倾斜角的取值范围.
考点:直线的斜率,直线的倾斜角
专题:直线与圆
分析:由于a>0,可得直线L:(a2+1)x+2ay+1=0(a>0)变为y=-
x-
.设直线的倾斜角为α(α∈[0,π)),则tanα=-
≤-
=-1.再利用正切函数的单调性即可得出.
| a2+1 |
| 2a |
| 1 |
| 2a |
| a2+1 |
| 2a |
| 2a |
| 2a |
解答:
解:∵a>0,
∴直线L:(a2+1)x+2ay+1=0(a>0)变为y=-
x-
.
设直线的倾斜角为α(α∈[0,π)).
则tanα=-
≤-
=-1.当且仅当a=1时取等号.
∴α∈(
,
].
∴直线斜率和倾斜角的取值范围分别为(-∞,-1],(
,
].
∴直线L:(a2+1)x+2ay+1=0(a>0)变为y=-
| a2+1 |
| 2a |
| 1 |
| 2a |
设直线的倾斜角为α(α∈[0,π)).
则tanα=-
| a2+1 |
| 2a |
| 2a |
| 2a |
∴α∈(
| π |
| 2 |
| 3π |
| 4 |
∴直线斜率和倾斜角的取值范围分别为(-∞,-1],(
| π |
| 2 |
| 3π |
| 4 |
点评:本题考查了直线的斜率与倾斜角的关系、基本不等式的性质、正切函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知x,y满足
,则x2+y2的最大值为( )
|
| A、5 | B、9 | C、16 | D、25 |
方程lnx=6-2x的根必定属于区间( )
| A、(-2,1) | ||||
B、(
| ||||
C、(1,
| ||||
D、(
|
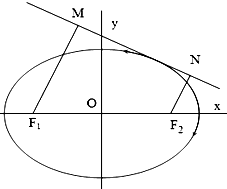 设点F1(-c,0),F2(c,0)分别是椭圆C:
设点F1(-c,0),F2(c,0)分别是椭圆C: