题目内容
已知sin2α=
,则cos2(α-
)=( )
| 1 |
| 5 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:二倍角的余弦
专题:三角函数的求值
分析:用二倍角的余弦公式可化简cos2(α-
)=
,已知sin2α=
,即可求值.
| π |
| 4 |
| 1+sin2α |
| 2 |
| 1 |
| 5 |
解答:
解:cos2(α-
)=
=
=
∵sin2α=
,
∴cos2(α-
)=
=
.
故选:B.
| π |
| 4 |
1+cos[2(α-
| ||
| 2 |
1+cos(2α-
| ||
| 2 |
| 1+sin2α |
| 2 |
∵sin2α=
| 1 |
| 5 |
∴cos2(α-
| π |
| 4 |
1+
| ||
| 2 |
| 3 |
| 5 |
故选:B.
点评:本题主要考察了二倍角的余弦公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
方程lnx=6-2x的根必定属于区间( )
| A、(-2,1) | ||||
B、(
| ||||
C、(1,
| ||||
D、(
|
将函数y=sin(4x-
)的图象先向左平移
,然后将所得图象上所有的点的横坐标变为原来的4倍(纵坐标不变),则所得到的图象对应的函数解析式为( )
| π |
| 3 |
| π |
| 12 |
| A、y=-cosx | ||
| B、y=sin4x | ||
| C、y=sinx | ||
D、y=sin(x-
|
已知f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a-1,2a],则y=f(x)的最大值为( )
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
在△ABC中,若AB=2,AC2+BC2=8,则△ABC面积的最大值为( )
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
把正整数按如图所示的规律排列,则从2003到2005的箭头方向依次为( )


| A、↓ 2004→ |
| B、↑ →2004 |
| C、2004→ ↑ |
| D、→2004 ↓ |
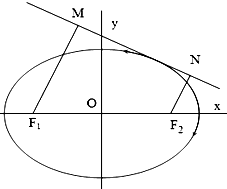 设点F1(-c,0),F2(c,0)分别是椭圆C:
设点F1(-c,0),F2(c,0)分别是椭圆C: