题目内容

求函数f（x）=log
1
2
3-2x-x2
的定义域和值域．
考点：对数函数的值域与最值
专题：函数的性质及应用
分析：由函数的解析式可得 3-2x-x2＞0，求得x的范围，可得函数的定义域．令t=3-2x-x2，利用二次函数的性质求得t的范围，可得log
1
2
t的范围，可得函数的值域．
解答： 解：由函数的解析式可得 3-2x-x2＞0，求得-3＜x＜1，故函数的定义域为（-3，1）．
令t=3-2x-x2=4-（x+1）2，则t∈（0，4]，∴log
1
2
t
∈[-1，+∞），
即函数的值域为[-1，+∞）．
点评：本题主要考查求复合函数的定义域和值域，函数的单调性、二次函数的性质的应用，属于基础题．
练习册系列答案
相关题目
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左右顶点分别为A，B，点P是双曲线C上不同于顶点的任意一点，若直线PA、PB的斜率之积为
1
2
．
（Ⅰ）求双曲线C的离心率e；
（Ⅱ）若过点P作斜率为k（k≠±
b
a
）的直线l，使得l与双曲线C有且仅有一个公共点，记直线PF1，PF2的斜率分别为k1，k2，问是否存在实数λ使得
1
k1
+
1
k2
=λk．
已知抛物线C的顶点在坐标原点，以坐标轴为对称轴，且焦点F（2，0）．
（1）求抛物线C的标准方程；
（2）直线l过焦点F与抛物线C相交与M，N两点，且|MN|=16，求直线l的方程．
已知直线l：kx-y+1+2k=0，求原点O到直线l距离的最大值．
已知直线y=-
1
2
x+2和椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）相交于A、B两点，M为线段AB的中点，若|AB|=2
5
，直线OM的斜率为
1
2
，求椭圆的方程．
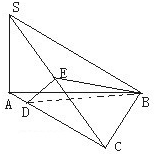已知SA⊥平面ABC，SA=AB，AB⊥BC，SB=BC，E是SC的中点，DE⊥SC交AC于D．
（1）求证：SC⊥面BDE；
（2）求二面角E-BD-C的大小．
椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，长轴端点与短轴端点间的距离为
5
，求椭圆C的方程．
如图，△ABC为直角三角形，BD⊥AC，证明：
AB•BC
AC
=BD．
已知数列{an}满足
u
=（an+1，n+1），
v
=（an，n）且
u
-
v
=λ（2，1）
（1）证明：数列{an}为等差数列；
（2）若数列{an}的首项a1为奇数，前n项和为Sn，若Sn最小值为-16，求a1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网