题目内容
如图1在直角梯形ABCD中,AB∥CD,AB⊥AD且AB=AD=
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻折,使平面ADEF与平面ABCD互相垂直如图2.

(1)求证:平面BDE⊥平面BEC;
(2)求直线BD与平面BEF所成角的正弦值.
| 1 |
| 2 |

(1)求证:平面BDE⊥平面BEC;
(2)求直线BD与平面BEF所成角的正弦值.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)由已知条件推导出ED⊥平面ABCD,BC⊥平面EBD,由此能证明平面EBD⊥平面EBC.
(2)由AD∥平面BEF,得D到平面BEF的距离与A到平面BEF的距离相等,过A作EB的垂线垂足为H,A到平面BEF的距离为AH,由此能求出直线BD与平面BEF所成角的正弦值.
(2)由AD∥平面BEF,得D到平面BEF的距离与A到平面BEF的距离相等,过A作EB的垂线垂足为H,A到平面BEF的距离为AH,由此能求出直线BD与平面BEF所成角的正弦值.
解答:
(本小题满分14分)
(1)证明:∵平面ADEF⊥平面ABCD,
又∵ADEF是正方形,∴ED⊥AD,∴ED⊥平面ABCD,
又∵平面EDB⊥平面ABCD,
又∵ABCD是直角梯形,AB∥CD,AB⊥AD,AB=AD=
CD=1,
得DB=BC=
,∴BD2+BC2=DC2,
∴∠DBC=90°,∴BC⊥BD,∴BC⊥平面EBD,
∴平面EBD⊥平面EBC.…(7分)
(2)解:∵ADEF是正方形,∴AD∥EF,
∵EF?平面BEF,AD?G平面BEF,∴AD∥平面BEF,
∴D到平面BEF的距离与A到平面BEF的距离相等,
又∵AD⊥AF,AD⊥AB,
∴AD⊥平面BEF,∵AD∥EF,∴EF⊥平面ABF,
∴平面ABF⊥平面BEF,
过A作EB的垂线垂足为H,则AH⊥平面BEF,
∴A到平面BEF的距离为AH,
∵AB=AF=1,∴AH=
,…(12分)
又∵BD=
,设BD与平面BEF所成角为θ,
则sinθ=
=
.…(14分)
(1)证明:∵平面ADEF⊥平面ABCD,
又∵ADEF是正方形,∴ED⊥AD,∴ED⊥平面ABCD,
又∵平面EDB⊥平面ABCD,
又∵ABCD是直角梯形,AB∥CD,AB⊥AD,AB=AD=
| 1 |
| 2 |
得DB=BC=
| 2 |
∴∠DBC=90°,∴BC⊥BD,∴BC⊥平面EBD,
∴平面EBD⊥平面EBC.…(7分)
(2)解:∵ADEF是正方形,∴AD∥EF,
∵EF?平面BEF,AD?G平面BEF,∴AD∥平面BEF,
∴D到平面BEF的距离与A到平面BEF的距离相等,
又∵AD⊥AF,AD⊥AB,
∴AD⊥平面BEF,∵AD∥EF,∴EF⊥平面ABF,
∴平面ABF⊥平面BEF,
过A作EB的垂线垂足为H,则AH⊥平面BEF,
∴A到平面BEF的距离为AH,
∵AB=AF=1,∴AH=
| ||
| 2 |
又∵BD=
| 2 |
则sinθ=
| AH |
| BD |
| 1 |
| 2 |
点评:本题主要考查直线与直线,直线与平面,平面与平面位置关系等基础知识;考查空间想象能力,推理论证能力和运算求解能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
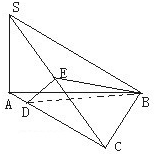 已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.
已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.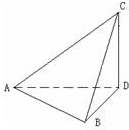 如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是
如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是