题目内容

求圆心在直线2x-y-3=0上，且过点A（5，2）和点B（3，2）的圆的方程．
考点：圆的标准方程
专题：直线与圆
分析：设圆心的坐标为C（a，2a-3），由|CA|=|CB|，求得a的值，可得圆心和半径，从而求得所求的圆的方程．
解答： 解：设圆心的坐标为C（a，2a-3），由点A（5，2）、点B（3，2），|CA|=|CB|，
可得 （a-5）2+（2a-3-2）2=（a-3）2+（2a-3-2）2，求得a=4，故圆心为（4，5），
半径为CA=
10
，故所求的圆的方程为 （x-4）2+（y-5）2=10．
点评：本题主要考查求圆的标准方程的方法，求出圆心坐标和半径的值，是解题的关键，属于基础题．
练习册系列答案
相关题目
设x、y满足约束条件
x+y≤1
y≥x
x≥0
，则z=2x-y的最大值为（　　）
A、0
B、2
C、3
D、
1
2
设函数f（x）=(x+1)2+2ln
1
x
．
（1）求f（x）的单调区间；
（2）若关于x的方程f（x）=x2+x+a+1在区间[1，3]上恰好有两个相异的实数根，求实数a的取值范围．
设函数f（x）=-x（x-a）2（x∈R），其中a∈R．
（1）当a=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；
（2）当a=3时，求函数f（x）的极小值．
已知抛物线C的顶点在坐标原点，以坐标轴为对称轴，且焦点F（2，0）．
（1）求抛物线C的标准方程；
（2）直线l过焦点F与抛物线C相交与M，N两点，且|MN|=16，求直线l的方程．
求函数g（x）=lnx+
1
x
的单调区间和最小值．
已知直线l：kx-y+1+2k=0，求原点O到直线l距离的最大值．
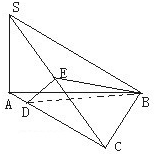已知SA⊥平面ABC，SA=AB，AB⊥BC，SB=BC，E是SC的中点，DE⊥SC交AC于D．
（1）求证：SC⊥面BDE；
（2）求二面角E-BD-C的大小．
已知函数f（x）=（x-a-1）ex+（b+1）x，g（x）=x2ex，a、b∈R．
（1）若b是函数g（x）的极大值点，求b的值；
（2）在（1）的条件下，若函数f（x）在（0，+∞）内存在单调递减区间，求a的取值范围；
（3）若x1＞0，x2＞0，且x1≠x2，求证：
ex1-ex2
x1-x2
＞e
x1+x2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网