题目内容
已知f（x）=2
sinxcosx+2cos2x-1（x∈R）
（1）求函数f（x）的最小正周期及在区间[0，
]上的最大值和最小值；
（2）若f（x0）=
，x0∈[
，
]，求cos（2x0+
）的值．
| 3 |
（1）求函数f（x）的最小正周期及在区间[0，
| π |
| 2 |
（2）若f（x0）=
| 6 |
| 5 |
| π |
| 4 |
| π |
| 2 |
| π |
| 6 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：三角函数的求值,三角函数的图像与性质
分析：（1）化简得f（x）=2sin（2x+
），求出函数的最小正周期以及最大、最小值；
（2）由（1）知，f(x0)=2sin(2x0+
)，求出sin（2x0+
）的值，考虑x0的取值范围，求出cos（2x0+
）的值．
| π |
| 6 |
（2）由（1）知，f(x0)=2sin(2x0+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答：
解：（1）由题知，f（x）=2
sinxcosx+2cos2x-1
=
sin2x+cos2x=2sin（2x+
），
∴函数的最小正周期为T=π；
∵x∈[0，
]，∴2x+
∈[
，
]，
∴f(x)max=f(
)=2 ，f(x)min=f(
)=-1；
（2）由（1）知，f(x0)=2sin(2x0+
)，
∴f（x0）=2sin（2x0+
）=
，
∴sin（2x0+
）=
，
∵x0∈[
，
]，
∴2x0+
∈[
，
]；
∴cos（2x0+
）＜0，
∴cos（2x0+
）=-
．
| 3 |
=
| 3 |
| π |
| 6 |
∴函数的最小正周期为T=π；
∵x∈[0，
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴f(x)max=f(
| π |
| 6 |
| π |
| 2 |
（2）由（1）知，f(x0)=2sin(2x0+
| π |
| 6 |
∴f（x0）=2sin（2x0+
| π |
| 6 |
| 6 |
| 5 |
∴sin（2x0+
| π |
| 6 |
| 3 |
| 5 |
∵x0∈[
| π |
| 4 |
| π |
| 2 |
∴2x0+
| π |
| 6 |
| 2π |
| 3 |
| 7π |
| 6 |
∴cos（2x0+
| π |
| 6 |
∴cos（2x0+
| π |
| 6 |
| 4 |
| 5 |
点评：本题考查了三角函数的求值问题以及三角函数的图象与性质的应用问题，解题时应细心作答，以免出错，是基础题．
练习册系列答案
相关题目
执行如图所示的程序框图，若输入的x值为
，则输出的y值为（ ）
| 1 |
| 4 |
| A、2 | |||
| B、-2 | |||
C、
| |||
D、
|
设x、y满足约束条件
，则z=2x-y的最大值为（ ）
|
| A、0 | ||
| B、2 | ||
| C、3 | ||
D、
|
下列命题中的假命题是（ ）
| A、以矩形的一边所在直线为旋转轴，其余三边旋转形成的曲面所围成的旋转体叫圆柱 |
| B、以直角三角形的一条边所在的直线为旋转轴，其余两边旋转形成的曲面的旋转体叫圆锥 |
| C、以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的曲面围成的旋转体叫圆锥 |
| D、以等腰三角形的底边上的高所在直线为旋转轴，其余各边旋转形成的曲面围成的旋转体叫圆锥 |
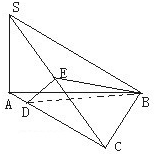已知SA⊥平面ABC，SA=AB，AB⊥BC，SB=BC，E是SC的中点，DE⊥SC交AC于D．