题目内容
已知函数f(x)=log2(x+a).
(1)若0<f(1-2x)-f(x)<
,当a=1时,求x的取值范围;
(2)若定义在R上奇函数g(x)满足g(x+2)=-g(x),且当0≤x≤1时,g(x)=f(x),求g(x)在[-3,-1]上的反函数h(x);
(3)对于(2)中的g(x),若关于x的不等式g(
)≥1-log23在R上恒成立,求实数t的取值范围.
(1)若0<f(1-2x)-f(x)<
| 1 |
| 2 |
(2)若定义在R上奇函数g(x)满足g(x+2)=-g(x),且当0≤x≤1时,g(x)=f(x),求g(x)在[-3,-1]上的反函数h(x);
(3)对于(2)中的g(x),若关于x的不等式g(
| t-2 x |
| 8+2 x+3 |
考点:对数函数图象与性质的综合应用,函数恒成立问题
专题:函数的性质及应用
分析:(1)根据对数函数的真数部分大于0,及对数的运算性质,可将不等式化为1<
<
,且2-2x>0且x+1>0,解不等式组可得x的取值范围;
(2)函数g(x)满足g(x+2)=-g(x),表示函数的周期为4,结合函数g(x)为奇函数,可求出x∈[-3,-1]时,函数g(x)的解析式,进而得到其反函数;
(3)利用对数函数的单调性及对数的运算性质,可将不等式转化log2(
-1)≥1-log23,由此可得实数t的取值范围.
| 2-2x |
| x+1 |
| 2 |
(2)函数g(x)满足g(x+2)=-g(x),表示函数的周期为4,结合函数g(x)为奇函数,可求出x∈[-3,-1]时,函数g(x)的解析式,进而得到其反函数;
(3)利用对数函数的单调性及对数的运算性质,可将不等式转化log2(
| 2x-t |
| 8+2x+3 |
解答:
解:(1)原不等式可化为0<log2(2-2x)-log2(x+1)<
,
∴1<
<
,且2-2x>0,且x+1>0,
得3-2
<x<
.
(2)∵g(x)是奇函数,∴g(0)=0,得a=1,
当x∈[-3,-1]时,-x-2∈[-1,1],
g(x)=-g(x+2)=g(-x-2)=log2(-x-1),
此时g(x)∈[-1,1],x=-2g(x)-1,
h(x)=-2x-1(x∈[-1,1]).
(3)∵x的不等式g(
)≥1-log23在R上恒成立,
∴log2(
-1)≥1-log23,
整理,得:3t=-37•2x-40<-77,
∴t<-
.
| 1 |
| 2 |
∴1<
| 2-2x |
| x+1 |
| 2 |
得3-2
| 2 |
| 1 |
| 3 |
(2)∵g(x)是奇函数,∴g(0)=0,得a=1,
当x∈[-3,-1]时,-x-2∈[-1,1],
g(x)=-g(x+2)=g(-x-2)=log2(-x-1),
此时g(x)∈[-1,1],x=-2g(x)-1,
h(x)=-2x-1(x∈[-1,1]).
(3)∵x的不等式g(
| t-2 x |
| 8+2 x+3 |
∴log2(
| 2x-t |
| 8+2x+3 |
整理,得:3t=-37•2x-40<-77,
∴t<-
| 77 |
| 3 |
点评:本题考查的知识点是对数函数的图象和性质,函数的奇偶性,函数的周期性,函数的单调性,反函数,对数的运算性质,存在性问题,函数的最值,是函数图象和性质较为综合的应用,难度较大.

练习册系列答案
相关题目
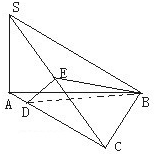 已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.
已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.