题目内容
过坐标原点作曲线y=lnx的切线l,该切线l与曲线y=lnx及x轴围成图形为D.
(1)求切线l的方程.
(2)求区域D的面积S.
(1)求切线l的方程.
(2)求区域D的面积S.
考点:定积分在求面积中的应用,利用导数研究曲线上某点切线方程
专题:综合题,导数的概念及应用
分析:(1)设出切点的坐标,根据设出的切点坐标和原点求出切线的斜率,同时由f(x)求出其导函数,把切点的横坐标代入导函数中即可表示出切线的斜率,两次求出的斜率相等列出关于a的方程,求出方程的解即可得到a的值,进而得到切点坐标,根据切点坐标和切线过原点写出切线方程即可;
(2)利用定积分表示面积,即可得出结论.
(2)利用定积分表示面积,即可得出结论.
解答:
解:(1)设切点坐标为(a,lna),
由切线过(0,0),得到切线的斜率k=
,
又f′(x)=
,把x=a代入得:斜率k=f′(a)=
,
所以
=
,得到lna=1,解得a=e,
则切点坐标为(e,1),
所以切线方程为:y=
x;
(2)S=
•1•
+
(
x-lnx)dx=
+(
x2-xlnx+x)
=
-1.
由切线过(0,0),得到切线的斜率k=
| lna |
| a |
又f′(x)=
| 1 |
| x |
| 1 |
| a |
所以
| lna |
| a |
| 1 |
| a |
则切点坐标为(e,1),
所以切线方程为:y=
| 1 |
| e |
(2)S=
| 1 |
| 2 |
| 1 |
| e |
| ∫ | e 1 |
| 1 |
| e |
| 1 |
| 2e |
| 1 |
| 2e |
| | | e 1 |
| e |
| 2 |
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,考查定积分知识,同时考查了运算求解的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
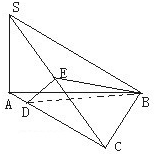 已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.
已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.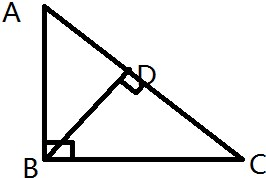
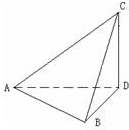 如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是
如图,将边长为1m的正△ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是