题目内容
在（1+x+x2）n=D
+D
x+D
x2+…+D
xr+…+D
x2n-1+D
x2n的展开式中，把D
，D
，D
，…，D
叫做三项式系数．
（1）当n=2时，写出三项式系数D
，D
，D
，D
，D
的值；
（2）类比二项式系数性质C
=C
+C
（1≤m≤n，m∈N，n∈N），给出一个关于三项式系数D
（1≤m≤2n-1，m∈N，n∈N）的相似性质，并予以证明；
（3）求D
C
-D
C
+D
C
-D
C
+…+D
C
的值．
0 n |
1 n |
2 n |
r n |
2n-1 n |
2n n |
0 1 |
1 n |
2 n |
2n n |
（1）当n=2时，写出三项式系数D
0 2 |
1 2 |
2 2 |
3 2 |
4 2 |
（2）类比二项式系数性质C
m n+1 |
m-1 n |
m n |
m+1 n+1 |
（3）求D
0 2014 |
0 2014 |
1 2014 |
1 2014 |
2 2014 |
2 2014 |
3 2014 |
3 2014 |
2014 2014 |
2014 2014 |
考点：二项式定理的应用
专题：排列组合,二项式定理
分析：（1）因为（1+x+x2）2=x4+2x3+3x2+2x+1，继而求得相应的值．
（2）类比二项式系数的性质可得三项式系数的性质，展开计算即可．
（3）分别写出（1+x+x2）2014和（x-1）2014的展开式，而（1+x+x2）2014（x-1）2014=（x3-1）2014，二项式（x3-1）2014 的通项Tr+1=
(x3)2014-r，得到的展开式中没有x2014项，问题得以解决．
（2）类比二项式系数的性质可得三项式系数的性质，展开计算即可．
（3）分别写出（1+x+x2）2014和（x-1）2014的展开式，而（1+x+x2）2014（x-1）2014=（x3-1）2014，二项式（x3-1）2014 的通项Tr+1=
| C | r 2014 |
解答：
解：（1）因为（1+x+x2）2=x4+2x3+3x2+2x+1，
所以
=1，
=2
=3
=2，
=1．
（2）类比二项式系数性质
=
+
（1≤m≤n，m∈N，n∈N），三项式系数有如下性质：
=
+
+
，（1≤m≤2n-1）
因为（1+x+x2）n+1=（1+x+x2）•（1+x+x2）n，
所以（1+x+x2）n+1=（1+x+x2）•（D
+D
x+D
x2+…+D
xr+…+D
x2n-1+D
x2n）．
上式左边xm+1的系数为
，
而上式右边xm+1的系数为
+
，
由（1+x+x2）n+1=（1+x+x2）•（1+x+x2）n为恒等式，得
：
=
+
+
，（1≤m≤2n-1）；
（3）∵（1+x+x2）2014=D
x0-D
x1+D
x2-D
x3+…+D
x2014，
（x-1）2014=C
x2014-C
x2013+C
x2012-…+C
．
∴（1+x+x2）2014（x-1）2014中x2014系数为D
C
-D
C
+D
C
-D
C
+…+D
C
，
又∴（1+x+x2）2014（x-1）2014=（x3-1）2014
而二项式（x3-1）2014 的通项Tr+1=
(x3)2014-r，
因为2014不是3的倍数，所以（x3-1）2014 的展开式中没有x2014项，
由代数式恒成立，得
D
C
-D
C
+D
C
-D
C
+…+D
C
=0．
所以
| D | 0 2 |
| D | 1 2 |
| ，D | 2 2 |
| ，D | 3 2 |
| D | 4 2 |
（2）类比二项式系数性质
| C | m n+1 |
| C | m-1 n |
| C | m n |
| D | m+1 n+1 |
| D | m-1 n |
| D | m n |
| D | m+1 n |
因为（1+x+x2）n+1=（1+x+x2）•（1+x+x2）n，
所以（1+x+x2）n+1=（1+x+x2）•（D
0 n |
1 n |
2 n |
r n |
2n-1 n |
2n n |
上式左边xm+1的系数为
| D | m+1 n+1 |
而上式右边xm+1的系数为
| D | m+1 n |
| +D | m n |
| D | m-1 n |
由（1+x+x2）n+1=（1+x+x2）•（1+x+x2）n为恒等式，得
：
| D | m+1 n+1 |
| D | m-1 n |
| D | m n |
| D | m+1 n |
（3）∵（1+x+x2）2014=D
0 2014 |
1 2014 |
2 2014 |
3 2014 |
2014 2014 |
（x-1）2014=C
0 2014 |
1 2014 |
2 2014 |
2014 2014 |
∴（1+x+x2）2014（x-1）2014中x2014系数为D
0 2014 |
0 2014 |
1 2014 |
1 2014 |
2 2014 |
2 2014 |
3 2014 |
3 2014 |
2014 2014 |
2014 2014 |
又∴（1+x+x2）2014（x-1）2014=（x3-1）2014
而二项式（x3-1）2014 的通项Tr+1=
| C | r 2014 |
因为2014不是3的倍数，所以（x3-1）2014 的展开式中没有x2014项，
由代数式恒成立，得
D
0 2014 |
0 2014 |
1 2014 |
1 2014 |
2 2014 |
2 2014 |
3 2014 |
3 2014 |
2014 2014 |
2014 2014 |
点评：本题主要考查二项式定理的应用，组合数的计算公式的应用，属于中档题．
练习册系列答案
相关题目
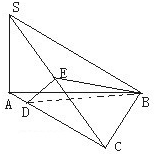已知SA⊥平面ABC，SA=AB，AB⊥BC，SB=BC，E是SC的中点，DE⊥SC交AC于D．