题目内容
17.在等差数列{an}中,a2=4,前4项之和为18.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设${b_n}=n•{2^{{a_n}-2}}$,求数列{bn}的前n项和Tn.
分析 (Ⅰ)利用已知条件列出方程组,求出首项与公差,即可求数列{an}的通项公式;
(Ⅱ)利用错位相减法求和,求解即可.
解答 (本小题满分12分)
解:(Ⅰ)设等差数列{an}的公差为d.
由已知得$\left\{\begin{array}{l}{a_1}+d=4\\ 4{a_1}+\frac{4×3}{2}d=18\end{array}\right.$…(2分)
解得$\left\{\begin{array}{l}{a_1}=3\\ d=1.\end{array}\right.$…(4分)
所以an=n+2.…(5分)
(Ⅱ)由(Ⅰ)可得bn=n•2n,…(6分)
∴Tn=b1+b2+b3+…+bn=1×2+2×22+3×23+…+n×2n①…(7分)
2Tn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1②…(8分)
①-②得:$-{T_n}=2+{2^2}+{2^3}+…+{2^n}-n×{2^{n+1}}$…(9分)
$-{T_n}=\frac{{2-{2^{n+1}}}}{1-2}-n×{2^{n+1}}=(1-n)×{2^{n+1}}-2$…(11分)
∴${T_n}=(n-1)×{2^{n+1}}+2$…(12分)
点评 本题考查数列求和,以及通项公式的求法,考查转化思想以及计算能力.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
8.对于给定的正整数数列{an},满足an+1=an+bn,其中bn是an的末位数字,下列关于数列{an}的说法正确的是( )
| A. | 如果a1是5的倍数,那么数列{an}与数列{2n}必有相同的项 | |
| B. | 如果a1不是5的倍数,那么数列{an}与数列{2n}必没有相同的项 | |
| C. | 如果a1不是5的倍数,那么数列{an}与数列{2n}只有有限个相同的项 | |
| D. | 如果a1不是5的倍数,那么数列{an}与数列{2n}有无穷多个相同的项. |
12.已知函数$f(x)=3cos(ωx+\frac{π}{3})(ω>0)$和g(x)=2sin(2x+φ)+1的图象的对称轴完全相同,若$x∈[0,\frac{π}{3}]$,则f(x)的取值范围是( )
| A. | [-3,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-3,\frac{{3\sqrt{3}}}{2}]$ | D. | $[-3,\frac{3}{2}]$ |
9.已知向量$\vec a=(3,-1)$,$\vec b=(1,x)$,且$\vec a⊥\vec b$,那么x的值是( )
| A. | -3 | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
6.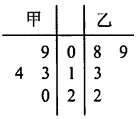 甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )
甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )
 甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )
甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )| A. | v1>v2,s1>s2 | B. | v1<v2,s1>s2 | C. | v1>v2,s1<s2 | D. | v1<v2,s1<s2 |