题目内容
6．
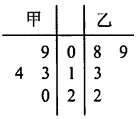甲乙两名篮球运动员在4场比赛中的得分情况如图所示．v1，v2分别表示甲、乙二人的平均得分，s1，s2分别表示甲、乙二人得分的方差，那么v1和v2，s1和s2的大小关系是（ ）| A． | v1＞v2，s1＞s2 | B． | v1＜v2，s1＞s2 | C． | v1＞v2，s1＜s2 | D． | v1＜v2，s1＜s2 |
分析 由茎叶图先求出平均数，再计算方差．
解答 解：由茎叶图性质得：
V1=$\frac{1}{4}（9+13+14+20）$=14，
V2=$\frac{1}{4}（8+9+13+22）$=13，
S1=$\frac{1}{4}$[（9-14）2+（13-14）2+（14-14）2+（20-14）2]=$\frac{31}{2}$，
S2=$\frac{1}{4}$[（8-13）2+（9-13）2+（13-13）2+（22-13）2]=$\frac{61}{2}$．
∴V1＞V2，S1＜S2．
故选：C．
点评 本题考查两组数据的平均数和方差的大小的比较，是基础题，解题时要认真审题，注意茎叶图的性质的合理运用．
练习册系列答案
相关题目
14．在△ABC中，a=2，c=1，∠B=60°，那么b等于（ ）
| A． | $\sqrt{5}$ | B． | $\sqrt{3}$ | C． | 1 | D． | $\frac{{\sqrt{3}}}{2}$ |
1．在“二十四节气入选非遗”宣传活动中，从甲、乙、丙三位同学中任选两人介绍一年中时令、气候、物候等方面的变化规律，那么甲同学被选中的概率为（ ）
| A． | 1 | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
16．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（b＞a＞0）$的左焦点F1（-c，0）（c＞0）作圆x2+y2=$\frac{{a}^{2}}{4}$的切线，切点为E，延长F1E交双曲线右支于点P．若E是F1P中点，则双曲线的离心率为（ ）
| A． | $\frac{5}{2}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\frac{\sqrt{5}+1}{2}$ | D． | $\frac{\sqrt{10}}{2}$ |