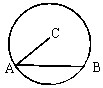
题目内容
如图,在半径为R的圆C中,已知弦AB的长为5,则
•
=( )
| AB |
| AC |

A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据AC为半径,C圆心,AB为弦,可得
在
上的投影为
|
|,再根据
•
=
|
|•|
|,计算求得结果.
| AC |
| AB |
| 1 |
| 2 |
| AB |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| AB |
解答:
解:由于AC为半径,C圆心,AB为弦,故
在
上的投影为
|
|,
∴
•
=
|
|•|
|=
×5×5=
,
故选:B.
| AC |
| AB |
| 1 |
| 2 |
| AB |
∴
| AB |
| AC |
| 1 |
| 2 |
| AB |
| AB |
| 1 |
| 2 |
| 25 |
| 2 |
故选:B.
点评:本题主要考查两个向量的数量积的定义,一个向量在另一个向量上的投影的定义,属于中档题.

练习册系列答案
相关题目
已知i是虚数单位,若
=1-i,则z的共轭复数为( )
| 3+i |
| z |
| A、1-2i | ||||
| B、2-4i | ||||
C、
| ||||
| D、1+2i |
设集合A={x|x2-3x+4≥0},集合B={x|log2x>1},则A∩∁RB=( )
| A、(-∞,2) |
| B、(-∞,2] |
| C、(0,2) |
| D、(0,2] |