Question

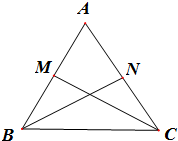在△ABC中，AB=4，AC=3，M，N分别是AB，AC的中点．
（Ⅰ）若A=60°，用

AB

，

AC

表示

BN

，

CM

，并求

BN

•

CM

的值；
（Ⅱ）若

BN

⊥

CM

，求cos（A+

π

3

）的值．

Answer 1

考点：向量在几何中的应用

专题：平面向量及应用

分析：（Ⅰ）利用向量的三角形法则和共线定理即可得出，再利用数量积的定义可得．再利用数量积的性质可得．
（Ⅱ）由BN⊥CM，可得

BN

•

CM

=0，再利用（Ⅰ）和向量的夹角公式即可得出cosA的值，再根据三角函数的和差公式求出即可．

解答： 解：（I）∵M，N分别是AB，AC的中点，
∴

BN

=

BA

+

AN

=-

AB

+

1

2

AC

，

CM

=

AM

-

AC

=

1

2

AB

-

AC

，
∵∠BAC=60°，AB=4，AC=3，
∴

AB

•

AC

=|

AB

|•|

AC|

cosA=4×3×cos60°=6．
∴

BN

•

CM

=（-

AB

+

1

2

AC

）•（

1

2

AB

-

AC

）=

5

4

AB

•

AC

-

1

2

AB

2-

1

2

AC

2=

5

2

×6-

1

2

×4²-

1

2

×3²=-5
（Ⅱ）由（Ⅰ）得

BN

•

CM

=

5

4

AB

•

AC

-

1

2

AB

2-

1

2

AC

2，
∵

BN

⊥

CM

，
∴

BN

•

CM

=0，
即

5

4

AB

•

AC

-

1

2

AB

2-

1

2

AC

2=0
∴

AB

•

AC

=10，
∴10=4×3×cosA，
∴cosA=

5

6

，
∴sinA=

11

6

，
∴cos（A+

π

3

）=cosAcos

π

3

-sinAsin

π

3

=

5

6

×

1

2

-

11

6

×

3

2

=

5- 33

12

点评：本题考查了向量的三角形法则、和共线定理、数量积的定义及其性质、向量垂直与数量积的关系、向量的夹角公式等基础知识与基本技能方法，考查了推理能力和计算能力，属于中档题