题目内容
已知PD垂直于平行四边形ABCD所在的平面,若PB⊥AC 平行四边形ABCD一定是 .
考点:直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:根据题意,画出图形,利用线面平行的判定定理和性质定理,可知AC⊥BD,由对角线互相垂直的平行四边形是菱形.即可得出结论.
解答:
 解:根据题意,画出图形如图,
解:根据题意,画出图形如图,
∵PD垂直平行四边形ABCD所在平面,
∴PD⊥AC,
又∵PB⊥AC,PD∩PB=P.
∴AC⊥平面PBD,
又∵BD?平面PBD,
∴AC⊥BD,
又ABCD是平行四边形,
∴平行四边形ABCD一定是菱形.
故答案为:菱形.
 解:根据题意,画出图形如图,
解:根据题意,画出图形如图,∵PD垂直平行四边形ABCD所在平面,
∴PD⊥AC,
又∵PB⊥AC,PD∩PB=P.
∴AC⊥平面PBD,
又∵BD?平面PBD,
∴AC⊥BD,
又ABCD是平行四边形,
∴平行四边形ABCD一定是菱形.
故答案为:菱形.
点评:此题考查学生的空间想象能力及线面垂直的判定与性质.由对角线互相垂直的平行四边形是菱形即可得出答案.

练习册系列答案
相关题目
函数y=-x2+2x-2的单调递减区间是( )
| A、(-∞,1] |
| B、[1,+∞) |
| C、(-∞,2] |
| D、[2,+∞) |
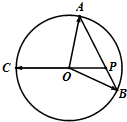 如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若
如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若| OC |
| OA |
| OB |
| A、(-1,0) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-1,0)∪(0,1) |
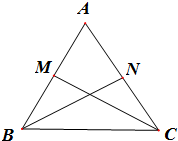 在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.
在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.