题目内容
22、已知函数f(x)=
x2-mlnx+(m-1)x,m∈R.
(1)若函数f(x)在x=2处取得极值,求m的值;
(2)当m≤0 时,讨论函数f(x) 的单调性;
(3)求证:当 m=-2时,对任意的1,x2∈(0,+∞),且x1≠x2,有
>-1.
| 1 |
| 2 |
(1)若函数f(x)在x=2处取得极值,求m的值;
(2)当m≤0 时,讨论函数f(x) 的单调性;
(3)求证:当 m=-2时,对任意的1,x2∈(0,+∞),且x1≠x2,有
| f(x 2)-f(x1) |
| x2-x1 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:函数思想,导数的综合应用
分析:(1)由题意,f′(2)=0,求出m的值;
(2)求出函数的导数f′(x),讨论m的值,当f′(x)>0时,f(x)增,f'(x)<0时,f(x)减;
(3)m=-2时,由函数f(x),构造辅助函数g(x)=f(x)+x,利用导数判断g(x)的单调性,
得出f(x1)+x1<f(x2)+x2,从而得出结论
>-1.
(2)求出函数的导数f′(x),讨论m的值,当f′(x)>0时,f(x)增,f'(x)<0时,f(x)减;
(3)m=-2时,由函数f(x),构造辅助函数g(x)=f(x)+x,利用导数判断g(x)的单调性,
得出f(x1)+x1<f(x2)+x2,从而得出结论
| f(x2)-f(x1) |
| x2-x1 |
解答:
解:(1)∵f(x)=
x2-mlnx+(m-1)x,m∈R,
∴f′(x)=x-
+m-1,
又∵函数 f(x)在x=2处有极值,
∴f′(2)=2-
+m-1=0,
解得m=-2;
(2)∵f′(x)=x-
+m-1=
=
,
∴①当-1<m≤0时,若x∈(0,-m)时,则f′(x)>0,f(x)为增函数;
当x∈(-m,1)时,f'(x)<0,f(x)为减函数,
当x∈(1,+∞)时,f'(x)>0,f(x)为增函数;
②当m=-1时,f′(x)=
≥0,f(x)在(0,+∞)上为增函数;
③当m<-1,即-m>1时,x∈(0,1)时,f'(x)>0,f(x)为增函数,
当x∈(1,-m)时,f'(x)<0,f(x)为减函数,
当x∈(-m,+∞)时,f'(x)>0,f(x)为增函数;
(3)当m=-2时,函数f(x)=
x2+2lnx-3x,
构造辅助函数g(x)=f(x)+x,并求导得:
g'(x)=x+
-2=
=
,
∴g'(x)>0,g(x)为增函数.
∴对任意0<x1<x2,都有g(x1)<g(x2)成立,
即f(x1)+x1<f(x2)+x2,
即f(x1)-f(x2)>x1-x2;
又∵x1-x2<0,
∴
>-1.(14分)
| 1 |
| 2 |
∴f′(x)=x-
| m |
| x |
又∵函数 f(x)在x=2处有极值,
∴f′(2)=2-
| m |
| 2 |
解得m=-2;
(2)∵f′(x)=x-
| m |
| x |
| x2+(m-1)x-m |
| x |
| (x-1)(x+m) |
| x |
∴①当-1<m≤0时,若x∈(0,-m)时,则f′(x)>0,f(x)为增函数;
当x∈(-m,1)时,f'(x)<0,f(x)为减函数,
当x∈(1,+∞)时,f'(x)>0,f(x)为增函数;
②当m=-1时,f′(x)=
| (x-1)2 |
| x |
③当m<-1,即-m>1时,x∈(0,1)时,f'(x)>0,f(x)为增函数,
当x∈(1,-m)时,f'(x)<0,f(x)为减函数,
当x∈(-m,+∞)时,f'(x)>0,f(x)为增函数;
(3)当m=-2时,函数f(x)=
| 1 |
| 2 |
构造辅助函数g(x)=f(x)+x,并求导得:
g'(x)=x+
| 2 |
| x |
| x2-2x+2 |
| x |
| (x-1)2+1 |
| x |
∴g'(x)>0,g(x)为增函数.
∴对任意0<x1<x2,都有g(x1)<g(x2)成立,
即f(x1)+x1<f(x2)+x2,
即f(x1)-f(x2)>x1-x2;
又∵x1-x2<0,
∴
| f(x2)-f(x1) |
| x2-x1 |
点评:本题考查了导数的综合应用问题,考查了函数的单调性与导数的关系,函数的极值与导数的关系,也考查了构造函数与转化思想,是综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=-x2+2x-2的单调递减区间是( )
| A、(-∞,1] |
| B、[1,+∞) |
| C、(-∞,2] |
| D、[2,+∞) |
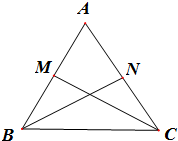 在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.
在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.