题目内容
定义在R上的函数f(x)满足对任意x,y∈R都有f(x+y)=f(x)+f(y).且x<0时,f(x)<0,f(-1)=-2
(1)求证:f(x)为奇函数;
(2)试问f(x)在x∈[-4,4]上是否有最值?若有,求出最值;若无,说明理由.
(3)若f(k•3x)+f(3x-9x-2)<0对任意x∈R恒成立,求实数k的取值范围.
(1)求证:f(x)为奇函数;
(2)试问f(x)在x∈[-4,4]上是否有最值?若有,求出最值;若无,说明理由.
(3)若f(k•3x)+f(3x-9x-2)<0对任意x∈R恒成立,求实数k的取值范围.
考点:抽象函数及其应用,函数的最值及其几何意义,函数恒成立问题
专题:计算题,证明题,函数的性质及应用
分析:(1)令x=y=0,再令y=-x,分别代入f(x+y)=f(x)+f(y)(x,y∈R),化简可得;
(2)由单调性的定义可证明函数f(x)为R上的增函数,从而求f(x)在x∈[-4,4]上的最值;
(3)(法一)由(2)知,f(k•3x)+f(3x-9x-2)<0可化为k•3x<-3x+9x+2,即32x-(1+k)•3x+2>0对任意x∈R成立.令t=3x>0,问题等价于t2-(1+k)t+2>0对任意t>0恒成立.令令g(t)=t2-(1+k)t+2,讨论二次函数的最值,从而求k;
(法二)由分离系数法,化k•3x<-3x+9x+2为k<3x+
-1,令u=3x+
-1,利用基本不等式求最值,从而求k.
(2)由单调性的定义可证明函数f(x)为R上的增函数,从而求f(x)在x∈[-4,4]上的最值;
(3)(法一)由(2)知,f(k•3x)+f(3x-9x-2)<0可化为k•3x<-3x+9x+2,即32x-(1+k)•3x+2>0对任意x∈R成立.令t=3x>0,问题等价于t2-(1+k)t+2>0对任意t>0恒成立.令令g(t)=t2-(1+k)t+2,讨论二次函数的最值,从而求k;
(法二)由分离系数法,化k•3x<-3x+9x+2为k<3x+
| 2 |
| 3x |
| 2 |
| 3x |
解答:
解:(1)证明:f(x+y)=f(x)+f(y)(x,y∈R),①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
则有0=f(x)+f(-x).
即f(-x)=-f(x)对任意x∈R成立,
则f(x)是奇函数.
(2)解:设x1,x2∈R,且x1<x2,则x1-x2<0,从而f(x1-x2)<0,
又f(x1)-f(x2)=f(x1)+f(-x2)=f[x1+(-x2)]=f(x1-x2).
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)为R上的增函数,
∴当x∈[-4,4]时,f(x)必为增函数.
又由f(-1)=-2,得-f(1)=-2,∴f(1)=2
∴当x=-4时,f(x)min=f(-4)=-f(4)=-4f(1)=-8;
当x=4时,f(x)max=f(4)=4f(1)=8.
(3)(法一)解:由(2)f(x)在R上是增函数,又由(1)f(x)是奇函数.
f(k•3x)<-f(3x-9x-2)=f(-3x+9x+2),
即:k•3x<-3x+9x+2,
即:32x-(1+k)•3x+2>0对任意x∈R成立.
令t=3x>0,问题等价于t2-(1+k)t+2>0对任意t>0恒成立.
令g(t)=t2-(1+k)t+2,
当
≤0,即k≤-1时,
g(t)在(0,+∞)上单调递增,
f(0)=2>0,符合题意;
当
>0,即k>-1时,
,
∴-1<k<-1+2
,
综上所述,当k<-1+2
时,
f(k•3x)+f(3x-9x-2)<0对任意x∈R恒成立.
(法二)(分离系数)由k•3x<-3x+9x+2得,
k<3x+
-1,
则u=3x+
-1≥2
-1,
(当且仅当3x=
,即3x=
时,等号成立)
故k<2
-1.
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
则有0=f(x)+f(-x).
即f(-x)=-f(x)对任意x∈R成立,
则f(x)是奇函数.
(2)解:设x1,x2∈R,且x1<x2,则x1-x2<0,从而f(x1-x2)<0,
又f(x1)-f(x2)=f(x1)+f(-x2)=f[x1+(-x2)]=f(x1-x2).
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)为R上的增函数,
∴当x∈[-4,4]时,f(x)必为增函数.
又由f(-1)=-2,得-f(1)=-2,∴f(1)=2
∴当x=-4时,f(x)min=f(-4)=-f(4)=-4f(1)=-8;
当x=4时,f(x)max=f(4)=4f(1)=8.
(3)(法一)解:由(2)f(x)在R上是增函数,又由(1)f(x)是奇函数.
f(k•3x)<-f(3x-9x-2)=f(-3x+9x+2),
即:k•3x<-3x+9x+2,
即:32x-(1+k)•3x+2>0对任意x∈R成立.
令t=3x>0,问题等价于t2-(1+k)t+2>0对任意t>0恒成立.
令g(t)=t2-(1+k)t+2,
当
| 1+k |
| 2 |
g(t)在(0,+∞)上单调递增,
f(0)=2>0,符合题意;
当
| 1+k |
| 2 |
|
∴-1<k<-1+2
| 2 |
综上所述,当k<-1+2
| 2 |
f(k•3x)+f(3x-9x-2)<0对任意x∈R恒成立.
(法二)(分离系数)由k•3x<-3x+9x+2得,
k<3x+
| 2 |
| 3x |
则u=3x+
| 2 |
| 3x |
| 2 |
(当且仅当3x=
| 2 |
| 3x |
| 2 |
故k<2
| 2 |
点评:本题考查了抽象函数的奇偶性的证明及函数的最值的求法,同时考查了恒成立问题的处理,属于难题.

练习册系列答案
相关题目
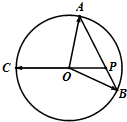 如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若
如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若| OC |
| OA |
| OB |
| A、(-1,0) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-1,0)∪(0,1) |
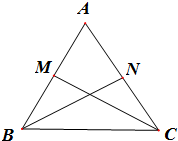 在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.
在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.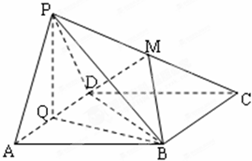 如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.