题目内容
如图所示，点O为△ABC的重心，且OA⊥OB，AB=6，则
•
=（ ）
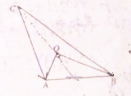
| AC |
| BC |
| A、36 | B、72 |
| C、108 | D、144 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由三角形的重心的向量表示，可得
=-（
+
），由向量的三角形法则，代入向量OC，再由向量垂直的条件和勾股定理，计算即可得到所求值．
| OC |
| OA |
| OB |
解答：
解：连接CO延长交AB于M，
则由O为重心，则M为中点，
且
=-2
=-2×
（
+
）=-（
+
），
由OA⊥OB，AB=6，则
•
=0，
2+
2=
2=36．
则
•
=（
-
）•（
-
）
=（2
+
）（2
+
）=5
•
+2（
2+
2）
=0+2×36=72．
故选B．
则由O为重心，则M为中点，
且
| OC |
| OM |
| 1 |
| 2 |
| OA |
| OB |
| OA |
| OB |
由OA⊥OB，AB=6，则
| OA |
| OB |
| OA |
| OB |
| AB |
则
| AC |
| BC |
| OC |
| OA |
| OC |
| OB |
=（2
| OA |
| OB |
| OB |
| OA |
| OA |
| OB |
| OA |
| OB |
=0+2×36=72．
故选B．
点评：本题考查三角形重心的向量表示，考查向量垂直的条件，考查向量的平方即为模的平方，考查运算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若直线的倾斜角为120°，则直线的斜率为（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知函数f（x）=
，则y=f[f（x）]-4的零点为（ ）
|
A、-
| ||
B、
| ||
C、-
| ||
D、-
|