题目内容
已知椭圆T:
+
=1(a>b>0)经过点P(2,
),一个焦点F的坐标是(2,0).
(Ⅰ)求椭圆T的方程;
(Ⅱ)设直线l:y=kx+m与椭圆T交于A、B两点,O为坐标原点,椭圆T的离心率为e,若kOA•kOB=e2-1.
①求
•
的取值范围;
②求证:△AOB的面积为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(Ⅰ)求椭圆T的方程;
(Ⅱ)设直线l:y=kx+m与椭圆T交于A、B两点,O为坐标原点,椭圆T的离心率为e,若kOA•kOB=e2-1.
①求
| OA |
| OB |
②求证:△AOB的面积为定值.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)通过焦点的坐标求出c的值,得到a2=b2+4,从而有
+
=1,解方程求出b的值,从而求出椭圆的方程;
(Ⅱ)由直线和椭圆得(1+2k2)x2+4kmx+2m2-8=0,设出A,B的坐标,根据根与系数的关系表示出
•
,△AOB的面积,从而得到答案.
| 4 |
| b2+4 |
| 2 |
| b2 |
(Ⅱ)由直线和椭圆得(1+2k2)x2+4kmx+2m2-8=0,设出A,B的坐标,根据根与系数的关系表示出
| OA |
| OB |
解答:
解:(Ⅰ)∵焦点F的坐标是(2,0),即c2=4,
∴a2=b2+4,
∴
+
=1,
将(2,
)代入椭圆的方程得:
+
=1,解得:b2=4,
∴a2=8,
∴椭圆的方程是:
+
=1;
(Ⅱ)证明:将y=kx+m代入
+
=1整理得:
(1+2k2)x2+4kmx+2m2-8=0,
当△=16k2m2-4(1+2k2)(2m2-8)>0,
即8k2+4>m2时,
设A(x1,y1),B(x2,y2),
∴x1+x2=-
,x1•x2=
,
则y1y2=(kx1+m)(kx2+m)
=k2x1 x2+km(x1+x2)+m2
=
,
∵椭圆T的离心率e=
,
KOA•KOB=
•
=
=-
,
即
=-
,得:m2=4k2+2,
∴
•
=
=
,
当k=0时,
•
=-2,
当k→∞时,
•
→2,
∴-2≤
•
<2,
而△AOB的面积S=
|x1y2-x2y1|
=
•|x1-x2|
=
=2
.
∴a2=b2+4,
∴
| x2 |
| b2+4 |
| y2 |
| b2 |
将(2,
| 2 |
| 4 |
| b2+4 |
| 2 |
| b2 |
∴a2=8,
∴椭圆的方程是:
| x2 |
| 8 |
| y2 |
| 4 |
(Ⅱ)证明:将y=kx+m代入
| x2 |
| 8 |
| y2 |
| 4 |
(1+2k2)x2+4kmx+2m2-8=0,
当△=16k2m2-4(1+2k2)(2m2-8)>0,
即8k2+4>m2时,
设A(x1,y1),B(x2,y2),
∴x1+x2=-
| 4km |
| 1+2k2 |
| 2m2-8 |
| 1+2k2 |
则y1y2=(kx1+m)(kx2+m)
=k2x1 x2+km(x1+x2)+m2
=
| m2-8k2 |
| 1+2k2 |
∵椭圆T的离心率e=
| ||
| 2 |
KOA•KOB=
| y1 |
| x1 |
| y2 |
| x2 |
| y1y2 |
| x1x2 |
| 1 |
| 2 |
即
| m2-8k2 |
| 2m2-8 |
| 1 |
| 2 |
∴
| OA |
| OB |
| 3m2-8k2-8 |
| 1+2k2 |
| 4k2-2 |
| 1+2k2 |
当k=0时,
| OA |
| OB |
当k→∞时,
| OA |
| OB |
∴-2≤
| OA |
| OB |
而△AOB的面积S=
| 1 |
| 2 |
=
| |m| |
| 2 |
=
2
| ||
| 1+2k2 |
=2
| 2 |
点评:本题考查了椭圆的简单性质,考查了直线和椭圆的关系,考查定值问题,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
点(1,2)到直线y=2x+1的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知直线a∥平面α,则下列命题是假命题的是( )
| A、a与α内的无数条直线平行 |
| B、a与α内的所有直线都平行 |
| C、a与α内的无数条直线垂直 |
| D、a与α无公共点 |
如图所示,点O为△ABC的重心,且OA⊥OB,AB=6,则
•
=( )
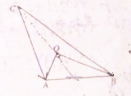
| AC |
| BC |

| A、36 | B、72 |
| C、108 | D、144 |