题目内容
空间的四点最多能确定 个平面．
考点：平面的基本性质及推论
专题：空间位置关系与距离
分析：根据空间四个点的位置关系进行判断即可．
解答：
解：若四个点共面，则只能确定一个平面，
若四个点不同在一个面上，则空间四点构成一个三棱锥，即四面体，此时有4个平面，
故答案为：4
若四个点不同在一个面上，则空间四点构成一个三棱锥，即四面体，此时有4个平面，
故答案为：4
点评：本题主要考查平面的基本性质，比较基础．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
已知向量
=（cosα，sinα），
=（2，3），若
∥
，则sin2α-sin2α的值等于（ ）
| a |
| b |
| a |
| b |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
a为正实数，i为虚数单位，|a+i|=2，则a=（ ）
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
已知双曲线
-y2=1（a＞0）的右焦点与抛物线y2=4
x的焦点重合，则此双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| 5 |
A、y=±
| ||||
| B、y=±2x | ||||
C、y=±
| ||||
D、y=±
|
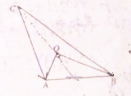
如图所示，点O为△ABC的重心，且OA⊥OB，AB=6，则
•
=（ ）
| AC |
| BC |
| A、36 | B、72 |
| C、108 | D、144 |
过双曲线
-
=1（a＞0，b＞0）的一个焦点F作渐近线的垂线，垂直为M，延长FM交y轴于E．若
=λ
（1＜λ＜2），则该双曲线的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| FE |
| FM |
| A、（1，2） | ||
| B、（2，+∞） | ||
C、（1，
| ||
D、（
|