题目内容
已知数列{an}满足a1=1,a2=3,an+2=3an+1-2an(n∈N+).
(Ⅰ)证明:数列{cn+1-an}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若数列{bn}满足4 h1-14 h2-1…4 hn-1=(an+1) bn(n∈N+),证明{bn}是等差数列.
(Ⅰ)证明:数列{cn+1-an}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若数列{bn}满足4 h1-14 h2-1…4 hn-1=(an+1) bn(n∈N+),证明{bn}是等差数列.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(Ⅰ)将an+2=3an+1-2an化为:
,由等比数列的定义进行证明即可;
(Ⅱ)由等比数列的通项公式得:an+1-an=2n,利用迭代法求出数列{an}的通项公式;
(Ⅲ)由指数的运算性质化简式子:4b1-14b2-1…4bn-1=(an+1)bn,给n恰当的值列出式子,再作差后得到数列{bn}的递推公式,由等差中项的性质进行证明.
|
(Ⅱ)由等比数列的通项公式得:an+1-an=2n,利用迭代法求出数列{an}的通项公式;
(Ⅲ)由指数的运算性质化简式子:4b1-14b2-1…4bn-1=(an+1)bn,给n恰当的值列出式子,再作差后得到数列{bn}的递推公式,由等差中项的性质进行证明.
解答:
(I)证明:∵an+2=3an+1-2an,∴
,
∵
,∴
,
∴{an+1-an}是以a2-a1=2为首项,2为公比的等比数列.…(4分)
(II)解:由(I)得an+1-an=2n(n∈N*),
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
…(8分)
(III)证明:∵4b1-14b2-1…4bn-1=(an+1)bn,
∴4(b1+b2+…+bn)=2nbn,
∴2[(b1+b2+…+bn)-n]=nbn,①
2[(b1+b2+…+bn+bn+1)-(n+1)]=(n+1)bn+1.②
由②-①得,2(bn+1-1)=(n+1)bn+1-nbn,
即(n-1)bn+1-nbn+2=0.③
nbn+2-(n+1)bn+1+2=0.④
由④-③得,nbn+2-2nbn+1+nbn=0,
即bn+2-2bn+1+bn=0,∴bn+2-bn+1=bn+1-bn(n∈N*),
∴{bn}是等差数列.…(14分)
|
∵
|
|
∴{an+1-an}是以a2-a1=2为首项,2为公比的等比数列.…(4分)
(II)解:由(I)得an+1-an=2n(n∈N*),
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
|
|
(III)证明:∵4b1-14b2-1…4bn-1=(an+1)bn,
∴4(b1+b2+…+bn)=2nbn,
∴2[(b1+b2+…+bn)-n]=nbn,①
2[(b1+b2+…+bn+bn+1)-(n+1)]=(n+1)bn+1.②
由②-①得,2(bn+1-1)=(n+1)bn+1-nbn,
即(n-1)bn+1-nbn+2=0.③
nbn+2-(n+1)bn+1+2=0.④
由④-③得,nbn+2-2nbn+1+nbn=0,
即bn+2-2bn+1+bn=0,∴bn+2-bn+1=bn+1-bn(n∈N*),
∴{bn}是等差数列.…(14分)
点评:本题考查等比、等差数列的证明方法:定义法、等差中项的性质,等差数列的通项公式,以及指数的额运算性质,考查化简、变形能力,难度较大.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
已知双曲线
-y2=1(a>0)的右焦点与抛物线y2=4
x的焦点重合,则此双曲线的渐近线方程为( )
| x2 |
| a2 |
| 5 |
A、y=±
| ||||
| B、y=±2x | ||||
C、y=±
| ||||
D、y=±
|
如图所示,点O为△ABC的重心,且OA⊥OB,AB=6,则
•
=( )
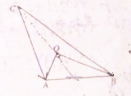
| AC |
| BC |

| A、36 | B、72 |
| C、108 | D、144 |
过双曲线
-
=1(a>0,b>0)的一个焦点F作渐近线的垂线,垂直为M,延长FM交y轴于E.若
=λ
(1<λ<2),则该双曲线的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| FE |
| FM |
| A、(1,2) | ||
| B、(2,+∞) | ||
C、(1,
| ||
D、(
|
焦点在y轴上,焦距是18,离心率e=
的双曲线方程是( )
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|