题目内容
已知数列{an}的前n项和为Sn,对任意n∈N*,满足Sn=2n+1-2,数列bn=log2an.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列cn=
,求数列{cn}的前项和 Tn.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列cn=
| 1 |
| bnbn+1 |
考点:数列的求和,数列递推式
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)根据数列的递推关系即可求数列{an},{bn}的通项公式;
(Ⅱ)利用裂项法即可求数列{bn}的前 n项和为 Tn.
(Ⅱ)利用裂项法即可求数列{bn}的前 n项和为 Tn.
解答:
解:(Ⅰ)当n≥2时,则an=Sn-Sn-1=2n+1-2-2n+2=2n,
当n=1时,a1=S1=22-2=4-2=2,满足an=2n,
故数列{an}的通项公式为an=2n;
则bn=log2an=log22n=n.
(Ⅱ)cn=
=
=
-
,
则数列{cn}的前项和 Tn=1-
+
-
+…+
-
=1-
=
.
当n=1时,a1=S1=22-2=4-2=2,满足an=2n,
故数列{an}的通项公式为an=2n;
则bn=log2an=log22n=n.
(Ⅱ)cn=
| 1 |
| bnbn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则数列{cn}的前项和 Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题主要考查等差数列的通项公式、等比数列的通项公式、裂项相消法求数列的前n项和,考查运算求解能力和函数与方程思想.

练习册系列答案
相关题目
如图所示,点O为△ABC的重心,且OA⊥OB,AB=6,则
•
=( )
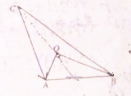
| AC |
| BC |

| A、36 | B、72 |
| C、108 | D、144 |
函数y=Asin(ωx+Φ)+k(A>0,ω>0,|Φ|<
)的图象如图所示,则y的表达式是( )
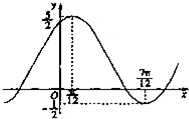
| π |
| 2 |

A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=sin(2x+
|