Question

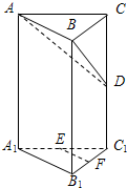在直三棱柱ABC-A₁B₁C₁中，如图所示，E、F分别为A₁C₁、B₁C₁的中点，D为棱CC₁的中点，G是棱AA₁上一点，且满足A₁G=mAA₁，若平面ABD∥平面GEF，试求m的值．

Answer 1

考点：平面与平面平行的判定

专题：空间位置关系与距离

分析：由平面ABD∥平面GEF，A、G、E、D四点共面，得GE∥AD，即可得出结论．

解答： 解：∵平面ABD∥平面GEF，A、G、E、D四点共面，
∴GE∥AD，
取AA₁的中点M，连结C₁M，则AD∥C₁M，
∴GE∥C₁M，∵E是A₁C₁的中点，∴G是A₁M的中点，
∴A₁G=

1

4

AA₁，
∴m=

1

4

．

点评：本题主要考查面面平行的性质的应用，属于基础题．