题目内容
过椭圆
+
=1的右焦点与y轴垂直的直线与椭圆相交于A、B两点，求|AB|的值．
| x2 |
| 13 |
| y2 |
| 12 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据a，b，c的关系，求出右焦点的坐标（1，0），把x=1代入椭圆的方程，从而求出|AB|的值．
解答：
解：∵a2=13，b2=12，∴c=1，
∴
+
=1，解得：y=±
，
∴|AB|=
．
∴
| 12 |
| 13 |
| y2 |
| 12 |
12
| ||
| 13 |
∴|AB|=
24
| ||
| 13 |
点评：本题考查了椭圆的性质，是一道基础题．
练习册系列答案
相关题目
函数y=f（x）是函数y=ax（a＞0）且a≠1的反函数，且y=f（x）图象经过点（9，2），则f（x）=（ ）
| A、log2x |
| B、log3x |
| C、2x |
| D、3x |
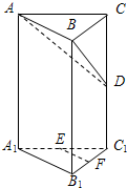在直三棱柱ABC-A1B1C1中，如图所示，E、F分别为A1C1、B1C1的中点，D为棱CC1的中点，G是棱AA1上一点，且满足A1G=mAA1，若平面ABD∥平面GEF，试求m的值．