题目内容
已知函数f(x)=ax3+bx2,当x=1时,f(x)的极值为3.
(1)求a,b的值;
(2)求该函数的解析式;
(3)若对于任意x∈(0,+∞),都有f(x)+mx<0成立,求实数m的取值范围.
(1)求a,b的值;
(2)求该函数的解析式;
(3)若对于任意x∈(0,+∞),都有f(x)+mx<0成立,求实数m的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:函数的性质及应用
分析:(1)先求导数,根据f(1)=3,f′(1)=0列出方程求出a,b;
(2)结合(1)可得f(x);
(3)是一个不等式恒成立问题,先将m分离出来,然后转化为函数的最值问题来解.
(2)结合(1)可得f(x);
(3)是一个不等式恒成立问题,先将m分离出来,然后转化为函数的最值问题来解.
解答:
解(1)因为f(x)=ax3+bx2,所以f′(x)=3ax2+2bx.
又因为当x=1时,f(x)的极值为3,所以
,
解得a=-6,b=9.
(2)由(1)可知f(x)=-6x3+9x2.
所以f′(x)=-18x2+18x=-18x(x-1).
令f′(x)>0得,0<x<1;令f′(x)<0得x<0或x>1.
故原函数的增区间为[0,1],减区间为(-∞,0),(1,+∞).
(3)由已知得f(x)+mx<0在(0,+∞)上恒成立.
即-6x3+9x2+mx<0在(0,+∞)上恒成立.
整理得m<6x2-9x=6(x-
)2-
(x>0)恒成立.
显然x=
时,上式右边二次函数取得最小值-
.
故m<-
即为所求.
又因为当x=1时,f(x)的极值为3,所以
|
解得a=-6,b=9.
(2)由(1)可知f(x)=-6x3+9x2.
所以f′(x)=-18x2+18x=-18x(x-1).
令f′(x)>0得,0<x<1;令f′(x)<0得x<0或x>1.
故原函数的增区间为[0,1],减区间为(-∞,0),(1,+∞).
(3)由已知得f(x)+mx<0在(0,+∞)上恒成立.
即-6x3+9x2+mx<0在(0,+∞)上恒成立.
整理得m<6x2-9x=6(x-
| 3 |
| 4 |
| 27 |
| 8 |
显然x=
| 3 |
| 4 |
| 27 |
| 8 |
故m<-
| 27 |
| 8 |
点评:本题考查了导数在研究函数单调性、极值时的应用.第三问涉及到的不等式恒成立问题,一般转化为函数的最值问题来解,能分离参数的尽量分离参数.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
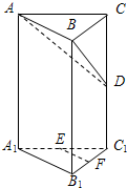 在直三棱柱ABC-A1B1C1中,如图所示,E、F分别为A1C1、B1C1的中点,D为棱CC1的中点,G是棱AA1上一点,且满足A1G=mAA1,若平面ABD∥平面GEF,试求m的值.
在直三棱柱ABC-A1B1C1中,如图所示,E、F分别为A1C1、B1C1的中点,D为棱CC1的中点,G是棱AA1上一点,且满足A1G=mAA1,若平面ABD∥平面GEF,试求m的值.