题目内容
若f（x）=ax2+（2a+b）x+2（其中x∈[2a-1，a+4]）是偶函数，则实数b= ．
考点：函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：由题意，定义域关于原点对称，f（x）=ax2+（2a+b）x+2=-x2+（-2+b）x+2中-2+b=0．
解答：
解：由函数f（x）=ax2+（2a+b）x+2（其中x∈[2a-1，a+4]）是偶函数，
故定义域关于原点对称，即2a-1=-（a+4），
可得a=-1．
于是函数f（x）=ax2+（2a+b）x+2=-x2+（-2+b）x+2，
而要使该函数为偶函数，
则须-2+b=0，
即b=2．
故答案为：b=2．
故定义域关于原点对称，即2a-1=-（a+4），
可得a=-1．
于是函数f（x）=ax2+（2a+b）x+2=-x2+（-2+b）x+2，
而要使该函数为偶函数，
则须-2+b=0，
即b=2．
故答案为：b=2．
点评：本题考查了函数的奇偶性的应用与判断，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
三个数0.52，2
，log20.2的大小关系为（ ）
| 1 |
| 2 |
A、log20.2＜0.52＜2
| ||
B、0.52＜2
| ||
C、log20.2＜2
| ||
D、0.52＜log20.2＜2
|
为了解132名学生的学习情况，采用系统抽样的方法，从中抽取容量为11的样本，则分段的间隔为（ ）
| A、10 | B、11 | C、12 | D、13 |
函数y=f（x）是函数y=ax（a＞0）且a≠1的反函数，且y=f（x）图象经过点（9，2），则f（x）=（ ）
| A、log2x |
| B、log3x |
| C、2x |
| D、3x |
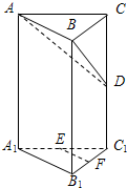在直三棱柱ABC-A1B1C1中，如图所示，E、F分别为A1C1、B1C1的中点，D为棱CC1的中点，G是棱AA1上一点，且满足A1G=mAA1，若平面ABD∥平面GEF，试求m的值．