题目内容
已知函数f（x）是定义在区间上[-2，2]的奇函数，且单调递增，满足f（t-2）+f（4-t2）＜0，则实数t的取值范围是 ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用,不等式的解法及应用
分析：根据函数的奇偶性和单调性，并且结合不等式f（t-2）+f（4-t2）＜0建立不等式进而求得t的范围．
解答：
解：由题意可得：奇函数f（x）在区间[-2，2]上是单调增函数，f（t-2）+f（4-t2）＜0，
所以f（t-2）＜f（t2-4），
所以
⇒
，解得：2＜x≤
．
故答案为：（2，
]．
所以f（t-2）＜f（t2-4），
所以
|
|
| 6 |
故答案为：（2，
| 6 |
点评：本题主要考查了函数奇偶性的应用，不等式的解法，注意函数的定义域．
练习册系列答案
智慧小复习系列答案
相关题目
三个数0.52，2
，log20.2的大小关系为（ ）
| 1 |
| 2 |
A、log20.2＜0.52＜2
| ||
B、0.52＜2
| ||
C、log20.2＜2
| ||
D、0.52＜log20.2＜2
|
函数y=f（x）是函数y=ax（a＞0）且a≠1的反函数，且y=f（x）图象经过点（9，2），则f（x）=（ ）
| A、log2x |
| B、log3x |
| C、2x |
| D、3x |
过点P1（-1，3），P2（2，5）的直线的斜率为（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
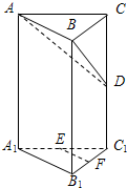在直三棱柱ABC-A1B1C1中，如图所示，E、F分别为A1C1、B1C1的中点，D为棱CC1的中点，G是棱AA1上一点，且满足A1G=mAA1，若平面ABD∥平面GEF，试求m的值．