题目内容
 如图,在多面体ABCDPQ中,底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,DQ∥AP,AP=AD=2DQ=2,
如图,在多面体ABCDPQ中,底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,DQ∥AP,AP=AD=2DQ=2,(1)求证:BD⊥平面PAC;
(2)求平面PAB与平面PCQ所成锐二面角的余弦值;
(3)若E为PB中点,点F在线段CQ上,当平面AEF⊥平面PAB时,求CF的长.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定,平面与平面垂直的性质
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明PA⊥BD,BD⊥AC,利用线面垂直的判定定理证明BD⊥平面PAC;
(2)建立坐标系,求出平面PAB的法向量、平面PCQ的法向量,利用向量的夹角公式求平面PAB与平面PCQ所成锐二面角的余弦值;
(3)设F(
(1-m),m+1,m),求出平面AEF的法向量,从而求出F的坐标,即可求出CF的长.
(2)建立坐标系,求出平面PAB的法向量、平面PCQ的法向量,利用向量的夹角公式求平面PAB与平面PCQ所成锐二面角的余弦值;
(3)设F(
| 3 |
解答:
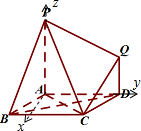 (1)证明:∵PA⊥底面ABCD,BD?底面ABCD,
(1)证明:∵PA⊥底面ABCD,BD?底面ABCD,
∴PA⊥BD,
∵底面ABCD为菱形,
∴BD⊥AC,
∵PA∩AC=A,
∴BD⊥平面PAC;
(2)解:建立如图所示的坐标系,则A(0,0,0),P(0,0,2),B(
,-1,0),C(
,1,0),Q(0,2,1)
∴
=(0,0,2),
=(
,-1,0),
设平面PAB的法向量为
=(x,y,z),则
,取
=(1,
,0),
同理可得平面PCQ的法向量为
=(
,1,2),
∴平面PAB与平面PCQ所成锐二面角的余弦值为
=
;
(3)解:设F(
(1-m),m+1,m),
∵E(
,-
,1),
∴
=(
,-
,1),
=(
(1-m),m+1,m),
设平面AEF的法向量为(a,b,1),则当平面AEF⊥平面PAB时,
,
∴a=-
,b=
,
∴平面AEF的法向量为(-
,
,1),
∴(-
)×
(1-m)+
(m+1)+m=0,
∴m=
,
∴F(
,
,
),
∴
=(-
,
,
),
∴|
|=
.
 (1)证明:∵PA⊥底面ABCD,BD?底面ABCD,
(1)证明:∵PA⊥底面ABCD,BD?底面ABCD,∴PA⊥BD,
∵底面ABCD为菱形,
∴BD⊥AC,
∵PA∩AC=A,
∴BD⊥平面PAC;
(2)解:建立如图所示的坐标系,则A(0,0,0),P(0,0,2),B(
| 3 |
| 3 |
∴
| AP |
| AB |
| 3 |
设平面PAB的法向量为
| m |
|
| m |
| 3 |
同理可得平面PCQ的法向量为
| n |
| 3 |
∴平面PAB与平面PCQ所成锐二面角的余弦值为
2
| ||||
|
| ||
| 4 |
(3)解:设F(
| 3 |
∵E(
| ||
| 2 |
| 1 |
| 2 |
∴
| AE |
| ||
| 2 |
| 1 |
| 2 |
| AF |
| 3 |
设平面AEF的法向量为(a,b,1),则当平面AEF⊥平面PAB时,
|
∴a=-
| ||
| 2 |
| 1 |
| 2 |
∴平面AEF的法向量为(-
| ||
| 2 |
| 1 |
| 2 |
∴(-
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴m=
| 1 |
| 3 |
∴F(
2
| ||
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
∴
| CF |
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴|
| CF |
| ||
| 3 |
点评:本题考查线面垂直,考查二面角的平面角,考查平面与平面垂直,考查学生分析解决问题的能力,有难度.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
为了解132名学生的学习情况,采用系统抽样的方法,从中抽取容量为11的样本,则分段的间隔为( )
| A、10 | B、11 | C、12 | D、13 |
过点P1(-1,3),P2(2,5)的直线的斜率为( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
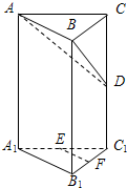 在直三棱柱ABC-A1B1C1中,如图所示,E、F分别为A1C1、B1C1的中点,D为棱CC1的中点,G是棱AA1上一点,且满足A1G=mAA1,若平面ABD∥平面GEF,试求m的值.
在直三棱柱ABC-A1B1C1中,如图所示,E、F分别为A1C1、B1C1的中点,D为棱CC1的中点,G是棱AA1上一点,且满足A1G=mAA1,若平面ABD∥平面GEF,试求m的值.