题目内容
四个面为全等正三角形的正四面体中，平行于一组相对棱，并平分其他各棱的截面是 ．
考点：平面的基本性质及推论
专题：空间位置关系与距离
分析：由题意做出相应的四面体和截面，利用三角形中位线定理可得四边形为平行四边形，由正四面体中相对棱垂直，得截面四边形为正方形．
解答：
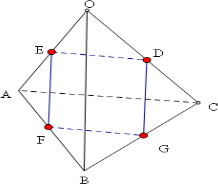解：如图做四个面为全等正三角形的正四面体O-ABC，
做截面DEFG平行于一组相对棱OB，AC，且平分其他各棱，
即D，E，F，G，为对应棱的中点，
由中位线的性质可得EF∥OB，DG∥OB，所以EF∥DG，
同理可得DE∥FG，
所以四边形DEFG为平行四边形，
由题意，正四面体中相对棱是垂直的，即OB⊥AC
所以是四边形DEFG正方形．
故答案为；正方形．
解：如图做四个面为全等正三角形的正四面体O-ABC，做截面DEFG平行于一组相对棱OB，AC，且平分其他各棱，
即D，E，F，G，为对应棱的中点，
由中位线的性质可得EF∥OB，DG∥OB，所以EF∥DG，
同理可得DE∥FG，
所以四边形DEFG为平行四边形，
由题意，正四面体中相对棱是垂直的，即OB⊥AC
所以是四边形DEFG正方形．
故答案为；正方形．
点评：数形结合，利用图形解题可将条件直观显现，利于我们观察，也辅助我们的空间想象力．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
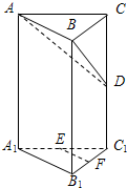在直三棱柱ABC-A1B1C1中，如图所示，E、F分别为A1C1、B1C1的中点，D为棱CC1的中点，G是棱AA1上一点，且满足A1G=mAA1，若平面ABD∥平面GEF，试求m的值．