题目内容
若函数f(x)满足:2f(x)+f(
)=3x,则f(x)+f(
)的值域为 .
| 1 |
| x |
| 1 |
| x |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:本题可以先求出函数f(x)的解析式,再求出函数f(x)+f(
)的解析式,从而求出f(x)+f(
)的值域,得到本题结论.
| 1 |
| x |
| 1 |
| x |
解答:
解:∵函数f(x)满足:2f(x)+f(
)=3x,
∴2f(
)+f(x)=
,
∴f(x)=2x-
,
f(
)=
-x,(x≠0),
∴f(x)+f(
)=x+
,(x≠0),
∵当x>0时,x+
≥2,
当x<0时,(-x)+
≥2,x+
≤-2,
∴f(x)+f(
)的值域为:(-∞,-2]∪[2,+∞).
故答案为:(-∞,-2]∪[2,+∞).
| 1 |
| x |
∴2f(
| 1 |
| x |
| 3 |
| x |
∴f(x)=2x-
| 1 |
| x |
f(
| 1 |
| x |
| 2 |
| x |
∴f(x)+f(
| 1 |
| x |
| 1 |
| x |
∵当x>0时,x+
| 1 |
| x |
当x<0时,(-x)+
| 1 |
| (-x) |
| 1 |
| x |
∴f(x)+f(
| 1 |
| x |
故答案为:(-∞,-2]∪[2,+∞).
点评:本题考查了函数的解析式和值域,本题难度不大,属于基础题.

练习册系列答案
相关题目
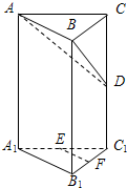 在直三棱柱ABC-A1B1C1中,如图所示,E、F分别为A1C1、B1C1的中点,D为棱CC1的中点,G是棱AA1上一点,且满足A1G=mAA1,若平面ABD∥平面GEF,试求m的值.
在直三棱柱ABC-A1B1C1中,如图所示,E、F分别为A1C1、B1C1的中点,D为棱CC1的中点,G是棱AA1上一点,且满足A1G=mAA1,若平面ABD∥平面GEF,试求m的值.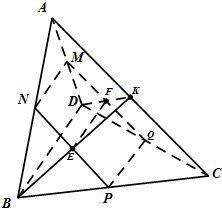 三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.
三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.