题目内容
设函数y=
,若函数在(-∞,1]上有意义,则实数a的取值范围是 .
| 1+2x+a•4x |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:使用换元令t=2x,将函数转化为一元二次函数y=1+t+at2进行求解.
解答:
解:设t=2x,因为x∈(-∞,1],所以0<t≤2.
则原函数有意义等价于1+t+at2≥0,所以a≥-
.
设f(t)=-
,则f(t)=-
=-(
+
)2+
,
因为0<t≤2,所以
∈[
,+∞),所以f(t)≤f(
)=-
,
所以a≥-
.
故答案为:[-
,+∞).
则原函数有意义等价于1+t+at2≥0,所以a≥-
| 1+t |
| t2 |
设f(t)=-
| 1+t |
| t2 |
| 1+t |
| t2 |
| 1 |
| t |
| 1 |
| 2 |
| 1 |
| 4 |
因为0<t≤2,所以
| 1 |
| t |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
所以a≥-
| 3 |
| 4 |
故答案为:[-
| 3 |
| 4 |
点评:本题考查了与指数函数有关的复合函数的最值问题,通过换元,将函数转化为一元二次函数,是解决本题的关键,对应不等式恒成立问题通常是转化为含参问题恒成立,即求函数的最值问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x-2),则当x<0时f(x)上的表达式为( )
| A、y=x(x-2) |
| B、y=x(x+2) |
| C、y=-x(x-2) |
| D、y=-x(x+2) |
已知=
(1,2),
=(0,1),
=(-2,k),若(
+2
)⊥
,则k=( )
| a |
| b |
| c |
| a |
| b |
| c |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
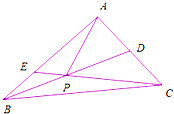 如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若
如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若