题目内容
已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x-2),则当x<0时f(x)上的表达式为( )
| A、y=x(x-2) |
| B、y=x(x+2) |
| C、y=-x(x-2) |
| D、y=-x(x+2) |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:本题利用函数的奇偶性,将自变量“x”转化为“-x”,然后利用条件当x≥0时,f(x)=x(x-2),求出函数解析式,得到本题结论.
解答:
解:∵函数y=f(x)是定义在R上的奇函数,
∴f(-x)=-f(x).
∵当x≥0时,f(x)=x(x-2),
∴当x<0时,-x>0,
f(x)=-f(-x)=-[(-x)•(-x-2)]=-x(x+2).
故选D.
∴f(-x)=-f(x).
∵当x≥0时,f(x)=x(x-2),
∴当x<0时,-x>0,
f(x)=-f(-x)=-[(-x)•(-x-2)]=-x(x+2).
故选D.
点评:本题考查了函数的奇偶性与解析式,本题难度不大,属于基础题.

练习册系列答案
相关题目
若f(x)=
,则f(f(-2))=( )
|
| A、2 | B、3 | C、4 | D、5 |
已知f(x)=x2-2|x|,则满足f[f(x)]=-
的实数x的个数为( )
| 1 |
| 2 |
| A、2 | B、4 | C、6 | D、8 |
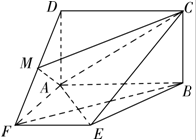 如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.
如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.