题目内容
化简:
+
.
| 1+cosθ-sinθ |
| 1-cosθ-sinθ |
| 1-cosθ-sinθ |
| 1+cosθ-sinθ |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:原式利用二倍角的余弦函数公式化简,提取公因式约分后,通分并利用同分母分式的加法法则计算,再利用同角三角函数间的基本关系及二倍角的正弦函数公式化简即可得到结果.
解答:
解:原式=
+
=
+
=-
-
=-
=-
2cos2
| ||||||
2sin2
|
2sin2
| ||||||
2cos2
|
2cos
| ||||||
2sin
|
2sin
| ||||||
2cos
|
cos
| ||
sin
|
sin
| ||
cos
|
| 1 | ||||
sin
|
| 2 |
| sinθ |
点评:此题考查了三角函数的化简求值,涉及的知识有:二倍角的正弦、余弦函数公式,同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键,属于基本知识的考查.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
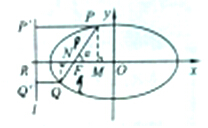 过椭圆
过椭圆