题目内容
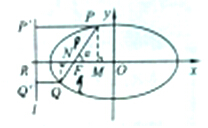过椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| p |
| 1 |
| q |
考点：椭圆的简单性质
专题：计算题,证明题,直线与圆,圆锥曲线的定义、性质与方程
分析：设P，Q在x轴上的射影分别为M，N，求出左准线方程，P，Q在准线上的射影分别为：P'，Q'，再由椭圆的第二定义，推出焦半径公式，再求倒数和，注意化简整理，结合离心率公式，a，b，c的关系，即可得到定值．
解答：
解：
+
为定值
．
证明如下：设P，Q在x轴上的射影分别为M，N，
左准线方程：x=-
，P，Q在准线上的射影分别为：P'，Q'．
设∠PFM=θ，则FM=pcosθ，FN=qcosθ，
由于e=
，则PF=e（
+xP）=a+exP=a+e（pcosθ-c）=p，
解得，p=
，
由于e=
，则QF=e（
+xQ）=a+exQ=a+e（-qcosθ-c）=q，
解得，q=
，
则有
+
=
=
=
=
．
| 1 |
| p |
| 1 |
| q |
| 2a |
| b2 |
证明如下：设P，Q在x轴上的射影分别为M，N，
左准线方程：x=-
| a2 |
| c |
设∠PFM=θ，则FM=pcosθ，FN=qcosθ，
由于e=
| PF |
| PP′ |
| a2 |
| c |
解得，p=
| a-ec |
| 1-ecosθ |
由于e=
| QF |
| QQ′ |
| a2 |
| c |
解得，q=
| a-ec |
| 1+ecosθ |
则有
| 1 |
| p |
| 1 |
| q |
| 1-ecosθ+1+ecosθ |
| a-ec |
=
| 2 |
| a-ec |
| 2 | ||
a-
|
=
| 2a |
| b2 |
点评：本题考查椭圆的性质和定义，考查椭圆的焦半径公式和离心率公式的运用，考查运算和化简整理能力，属于中档题和易错题．
练习册系列答案
相关题目
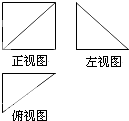如图，某几何体的正视图是边长为2的正方形，左视图和俯视图都是直角边长为2的等腰直角三角形，则该几何体的体积等于