题目内容
不等式|x-1|+|x+3|≥a恒成立,则a的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由条件利用绝对值三角不等式求得|x-1|+|x+3|的最小值为4,从而结合题意得到a的范围.
解答:
解:由于|x-1|+|x+3|≥|(x-1)-(x+3)|=4,不等式|x-1|+|x+3|≥a恒成立,
∴4≥a,
故答案为:(-∞,4].
∴4≥a,
故答案为:(-∞,4].
点评:本题主要考查绝对值三角不等式,函数的恒成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
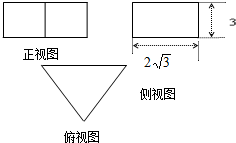 一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )
一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )A、4(9+2
| ||
B、(24+8
| ||
C、14
| ||
D、18
|
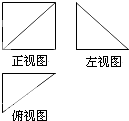 如图,某几何体的正视图是边长为2的正方形,左视图和俯视图都是直角边长为2的等腰直角三角形,则该几何体的体积等于
如图,某几何体的正视图是边长为2的正方形,左视图和俯视图都是直角边长为2的等腰直角三角形,则该几何体的体积等于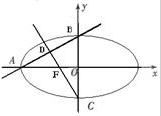 如图,椭圆
如图,椭圆