题目内容

解方程组：
a+b=9
2
c
a
=
3
5
a2=b2+c2
．
考点：有理数指数幂的化简求值
专题：计算题,函数的性质及应用
分析：利用代入法求解方程组．
解答： 解：解方程组
a+b=9
2
c
a
=
3
5
a2=b2+c2
得，
由二式得，c=
3
5
a，代入三式得；
a2=b2+
9
25
c2；
故|b|=
4
5
|a|；
若b=
4
5
a；
则
4
5
a+a=9
2
，
解得，a=5
2
，b=4
2
，c=3
2
．
若b=-
4
5
a，
则a-
4
5
a=9
2
，
则a=45
2
，b=-36
2
，c=27
2
．
点评：本题考查了方程组的解法，属于基础题．
练习册系列答案
相关题目
解方程：3x=2-x（精确到0.1）
下列命题中正确的是
 
（写出所有正确命题的序号）
①在直角三角形中，三条边的长成等差数列的充要条件是它们的比为3：4：5；
②设Sn是等比数列{an}的前n项和，则公比q=-
34
2
是数列S3，S9，S6成等差教列的充分不必要条件；
③若数列{an}满足a1=2，an+1=ancos
nπ
2
，则a2010=0；
④在数列{an}中，若a1，a2都是正整数，且an=|an-1-an-2|，n=3，4，5…，则称{an}为“绝对差数列”，则此数列中必含有为0的项．
设函数f（ex）=ex，g（x）=
1
e
f（x）-（x+1）（e=2.718…）
（1）求函数g（x）的极大值；
（2）令F（x）=
x2
2
-f（x），求函数y=F（x）的单调区间．
求函数y=cos（2x+
2π
7
）-2cos（x+
π
7
）的值域．
已知α为第四象限角，sinα+cosα=
7
13
，则tanα=
 
．
已知3sinβ=sin（2α+β）且tan（α+β）=4，则tanα=
 
．
化简：
1+cosθ-sinθ
1-cosθ-sinθ
+
1-cosθ-sinθ
1+cosθ-sinθ
．
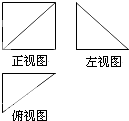如图，某几何体的正视图是边长为2的正方形，左视图和俯视图都是直角边长为2的等腰直角三角形，则该几何体的体积等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网