题目内容
已知函数f(x)=log9(9x+1)+kx(k∈R)是偶函数
(Ⅰ)求实数k的值;
(Ⅱ)设g(x)=
x+m(m∈R),问是否存在实数m,使得函数f(x)的图象恒在函数g(x)的图象上方?若存在,求m的取值范围;若不存在,请说明理由.
(Ⅰ)求实数k的值;
(Ⅱ)设g(x)=
| 1 |
| 2 |
考点:函数恒成立问题,函数奇偶性的性质
专题:函数的性质及应用
分析:(Ⅰ)因为f(x)为偶函数,所以f(-x)=f(x)代入,求得k的值即可;
(Ⅱ)函数f(x)的图象恒在函数g(x)的图象上方,从而f(x)-g(x)=log9(9x+1)-x-m>0恒成立,设F(x)=log9(9x+1)-x,求出函数F(x)的最小值,进而可求实数b的取值范围.
(Ⅱ)函数f(x)的图象恒在函数g(x)的图象上方,从而f(x)-g(x)=log9(9x+1)-x-m>0恒成立,设F(x)=log9(9x+1)-x,求出函数F(x)的最小值,进而可求实数b的取值范围.
解答:
解:(Ⅰ)因为y=f(x)为偶函数,
所以?x∈R,f(-x)=f(-x),
即log9(9-x+1)-kx=log9(9x+1)+kx对于?x∈R恒成立.
即2kx=log9(9-x+1)-log9(9x+1)=log9(
)-log9(9x+1)-x恒成立
∴(2k+1)x=0恒成立,
∵x不恒为零,
∴k=-
.
(Ⅱ)∵g(x)=
x+m,f(x)=log9(9x+1)-
x
∵函数f(x)的图象恒在函数g(x)的图象上方
∴f(x)-g(x)=log9(9x+1)-x-m>0恒成立,
∴m<log9(9x+1)-x恒成立,
设F(x)=log9(9x+1)-x=log9(9x+1)-log99x=log9(
+1)
任取x1、x2∈R,且x1<x2,则0<9x1<9x2,
>
于是log9(
+1)>log9(
+1)
,即F(x1)>F(x2),
所以F(x)在(-∞,+∞)是单调减函数.
∵
+1>1,
∴F(x)=log9(
+1)>0
∴m≤0
故m的取值范围是(-∞,0].
所以?x∈R,f(-x)=f(-x),
即log9(9-x+1)-kx=log9(9x+1)+kx对于?x∈R恒成立.
即2kx=log9(9-x+1)-log9(9x+1)=log9(
| 1+9x |
| 9x |
∴(2k+1)x=0恒成立,
∵x不恒为零,
∴k=-
| 1 |
| 2 |
(Ⅱ)∵g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
∵函数f(x)的图象恒在函数g(x)的图象上方
∴f(x)-g(x)=log9(9x+1)-x-m>0恒成立,
∴m<log9(9x+1)-x恒成立,
设F(x)=log9(9x+1)-x=log9(9x+1)-log99x=log9(
| 1 |
| 9x |
任取x1、x2∈R,且x1<x2,则0<9x1<9x2,
| 1 |
| 9x1 |
| 1 |
| 9x2 |
于是log9(
| 1 |
| 9x1 |
| 1 |
| 9x2 |
,即F(x1)>F(x2),
所以F(x)在(-∞,+∞)是单调减函数.
∵
| 1 |
| 9x |
∴F(x)=log9(
| 1 |
| 9x |
∴m≤0
故m的取值范围是(-∞,0].
点评:本题重点考查函数的性质,考查函数与方程的关系,解题的关键是正确运用偶函数的定义,合理将问题进行等价转化,属于中档题

练习册系列答案
相关题目
已知集合A={0,1,2},集合B={x,y|x∈A,y∈A,x+y∈A},则B的元素个数为( )
| A、5 | B、6 | C、7 | D、8 |
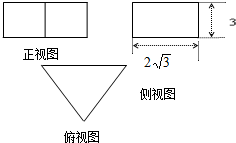 一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )
一个几何体的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该几何体的表面积为( )A、4(9+2
| ||
B、(24+8
| ||
C、14
| ||
D、18
|