题目内容
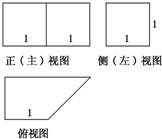
某空间几何体的三视图如图所示，则该几何体的表面积为（ ）
A、12+4
| ||
B、18+8
| ||
| C、28 | ||
D、20+8
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是直三棱柱，由三视图判断三棱柱的高，判断底面三角形的形状及相关几何量的数据，把数据代入表面积公式计算．
解答：
解：由三视图知：几何体是直三棱柱，且三棱柱的高为4，
底面是直角边长为2的等腰直角三角形，斜边长为
=2
，
∴几何体的表面积S=2×
×2×2+（2+2+2
）×4=4+16+8
=20+8
．
故选：D．
底面是直角边长为2的等腰直角三角形，斜边长为
| 4+4 |
| 2 |
∴几何体的表面积S=2×
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
故选：D．
点评：本题考查了由三视图求几何体的表面积，判断几何体的形状及数据所对应的几何量是解答此类问题的关键．
练习册系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的表面积为（ ）
A、6+
| ||
B、7+
| ||
C、8+
| ||
D、7+2
|
已知全集U=Z，A={-1，0，1，2}，B={x∈R|x2=3x-2}，则A∩（∁UB）=（ ）
| A、{-1，2} |
| B、{-1，0} |
| C、{0，1} |
| D、{1，2} |
已知函数f（x）=sin（ωx+φ），对任意的实数x均存在a使得f（a）≤f（x）≤f（0）成立，且|a|的最小值为
，则函数f（x）的单调递减区间为（ ）
| π |
| 2 |
A、[kπ-
| ||
B、[kπ，kπ+
| ||
C、[2kπ-
| ||
D、[2kπ，2kπ+
|
已知集合A={x|（x-1）（x-5）＜0}，B={x|log2x≤2}，则集合A∩B=（ ）
| A、{x|0＜x＜4} |
| B、{x|0＜x＜5} |
| C、{x|1＜x≤4} |
| D、{x|4≤x＜5} |
已知i是虚数单位，复数z满足：（1-2i）z=（1+i）2，则z的值是（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
函数f（x）=2
sinxcosx+
cos2x的最小正周期和振幅分别是（ ）
| 6 |
| 2 |
A、π，
| ||
B、π，
| ||
| C、2π，1 | ||
D、π，2
|
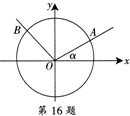如图，角α的始边与x轴的非负半轴重合，终边与单位圆交于点A （x1，yl），将射线OA按逆时针方向旋转